함수, 函數, function
수학에서 두 집합 사이의 관계를 설명하는 논리적 개념
간단하게 정의역의 원소마다 공역의 원소가 오직 하나씩 대응되는 관계를 말한다. 수학적 구조를 정의할 때는 물론 현실의 다양한 분야에서도 응용된다.
수학에서 함수(函數, 영어: function) 또는 사상(寫像, 영어: map, mapping)은 어떤 집합의 각 원소를 다른 집합의 유일한 원소에 대응시키는 것이다. 즉, 한 변수의 값에 따라 정해지는 다른 변수의 값을 먼저 주어지는 값에 상대하여 일컫는 말이다. 예를 들면, 집합 X의 원소 x 한 개에 집합 Y의 원소 y 한 개가 대응하는 관계를 의미한다. 거꾸로 y 한 개가 x 여러 개에 대응하는 관계도 함수라고 한다.
일상에서의 함수
보통 함수 하면 실수 집합(의 부분집합)을 정의역과 공역으로 갖는 실함수를 떠올리고, 이는 실생활에서 기대하는 함수의 역할인 한 변수에 대한 다른 변수의 변화의 기술에 사용된다. 역사적으로 함수는 미적분학의 주 목적인 시간에 따른 물체 위치의 변화를 기술하면서 따라나왔다. 이것이 단순히 시간적 변화뿐만이 아니라 관련있는 숫자 둘로 일반화된 것으로 볼 수 있다. 과학에서 나오는 법칙이라고 이름 붙은 것들 대부분은 따지고 보면 뭐가 변할 때 다른 하나가 변하는 함수의 형태로 나온다는 것을 관찰할 수 있다. 비단 과학법칙이 아니라도 연관있어 보이는 두 변수가 함수로 연관되어 있다고 생각하고, 그 함수를 식으로 나타내어 결과나 경향을 예측하는 것이 함수의 주된 쓰임 중 하나인 모델링이다. 이 함수의 증감추세를 그림으로 한눈에 표현하는 그래프는 덤이다. 이런 상황에선 x, y를 각각 독립변수(獨立變數, independent variable), 종속변수(從屬變數, dependent variable)라 부르는 경우가 많다. 흔히 말하는 '다변수함수'도 독립변수와 종속변수가 실수 여러 개로 늘어났다는 거 말고는 여기서 크게 벗어나지 않는다.
함수는 자연현상의 인과관계를 설명할 때 적합하다. 모든 현상(X)은 반드시 그에 따른 결과(Y)AA가 발생한다. 계속 똑같은 원인이 생기면 당연히 결과도 똑같으며, 뜬금없이 전혀 다른 결과가 생기는 경우는 없다. 컵 속 물을 예로 들자면, 우리가 일상생활에서 -30도에서 200도(정의역)까지 물의 온도를 특정한 값(X)으로 균일하게 조절하면 물은 고체/액체/기체 상태(Y)가 된다. 여기서 생각을 단순하게 해보자. 고체도 액체도 기체도 아닌 다른 상태로 존재하는 것이 가능할까? 뭐, 압력이 낮고 일정하다면 [-30, 200]에서는 일어나지 않는다. 이 부분에서 함수의 특징 중 하나인 모든 X는 반드시 그와 짝을 이루는 Y값이 있다라는 개념이 들어간다. 또 하나 생각해볼 게 있다. 임계 압력 이하에서[7] 과연 특정 온도의 물이 한 번에 두 가지 상태를 다 가지는 일이 있을 수 있을까? 상식적으로 생각해봐도 물은 액체이면 액체, 기체이면 기체여야 하며 액체이면서 기체인 경우는 말이 안 된다. 여기에 모든 X는 반드시 Y에 하나만 대응한다라는 개념이 포함되는 것이다.
물론 위의 문단은 예시일 뿐, 양자역학적 관점으로는 틀린 말이 된다. 불확정성 원리에 따르면 같은 사람이 던진 주사위라도 항상 같은 수가 나오지 않듯이 같은 조건(x)에서도 다른 결론(y)이 도출될 수 있다고 한다. 즉, '집합 X의 원소 하나에는 Y의 원소 하나만이 대응된다'라는 정의를 위반한 셈. 그리고 사실 액체이면서 기체, 기체이면서 액체인 경우는 존재하긴 한다. 일상생활에서는 보기 힘들 뿐, 애초에 함수 개념이 처음 제시된 때는 아직 양자역학이 들어서기 훨씬 전으로 한창 고전물리학이 태동하던 시기였단 걸 고려하자. 후술하겠지만 이러한 유형의 함수는 좀 더 넓은 의미의 함수와 관계되어 있다.
하지만 이렇게만 함수를 생각하며 고등수학의 정의를 보면 적잖은 괴리감을 느낄 것이다. 일반적인 함수는 정의역과 공역이 수의 집합일 필요도 없고, 따라서 그래프는커녕 '변수'니 '변화'니 하는 말부터 의미가 없다. 현대적인 함수의 정의는 수학자 디리클레 혹은 데데킨트의 정의[8]로, 굳이 식이니 변화니 하는 부분을 다 쳐내고 저렇게 추상적인 부분만 남긴 이유는 수학 중 해석학의 발전에 따른 수학자 수요가 일차적 원인이다. 간단히 말하면 식이나 변화(미분)의 요소가 없는 함수도 같이 생각을 해주는 게 더 일관성이 있었다. 자세한 이야기는 아래의 '함수의 역사' 부분에 서술.
물론 해석학 하나 때문에 저렇게 바꾼 건 아니다. 함수의 추상적 정의는 해석학 밖에 수학 여러 분야에서도 수가 포함되지 않는 광범위한 개념들을 함수로 편입시키며 큰 영향을 끼쳤다. 대학수학 정도만 가도 '함수의 공간'에서 '함수의 공간'으로의 '함수'[9]와 이상해 보이는 함수들이 마구 튀어나오는데, 익숙해지면 생각보다 유용하게 써먹을 곳이 많다. 일상생활과 관련이 많은 이산수학에서도 알고리즘, 관계, 분류 등을 생각할 때 여기저기서 튀어나온다. 프로그래밍 언어의 함수도 따지고 보면 여기서 비롯되었다.
함수(function)
f : X → Y는 f가 정의역 X, 공역 Y를 갖는 함수라는 의미로, 보통은 y = f(x)로 사용함.

위의 그림에서 집합 X는 함수 f의 정의역(domain)이라고 하며, 집합 Y는 함수 f의 공역(codomain)이라고 합니다.
이때 치역(range)이란 원소 x에 대응하는 집합 Y의 원소 f(x)를 모두 모은 집합을 의미합니다.
프로그래밍에서의 함수
프로그래밍에서 함수(function)란 특정 목적의 작업을 수행하기 위해 독립적으로 설계된 프로그램 코드의 집합으로 정의할 수 있습니다.
또한, 변수(variable)란 데이터를 저장하기 위해 프로그램에 의해 이름을 할당받은 메모리 공간을 의미합니다.

프로그래밍에서 함수를 사용하는 가장 큰 이유는 바로 반복적인 프로그래밍을 피할 수 있기 때문입니다.
또한, 프로그램을 여러 개의 함수로 나누어 작성하면, 모듈화로 인해 전체적인 코드의 가독성이 좋아집니다.
그리고 프로그램에 문제가 발생하거나 기능의 변경이 필요할 때에도 손쉽게 유지보수를 할 수 있습니다.
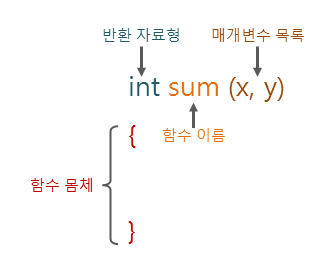
예제) C언어에서의 함수의 정의
역사
삼각함수와 같은 특정 함수에 대한 연구는 오래전부터 있어 왔다. 16세기 라이프치히 대학교의 수학 교수이자 코페르니쿠스의 《천구의 회전에 관하여》가 출간되는데 큰 역할을 하였던 레티쿠스는 1596년 《팔라티누스 삼각형 서(書)》(라틴어: Opus Palatinum de triangulis)에서 삼각함수표를 정리하여 발표하기도 하였다. 그러나 당시의 연구는 현재의 함수 정의에 확립되어 있는 관계에 대한 개념이 없이 단순히 계산의 편의를 도모하기 위한 것이었다. 한편, 르네 데카르트는 직교좌표계를 이용하여 오늘날 함수의 관계식에 해당하는 방정식을 그래프로 표현하는 방법을 제시하였다.
17세기에 도입한 대부분의 함수는 함수 개념이 충분히 인식되기 이전에는 곡선, 특히 운동 궤적으로서 연구되었다. 1667년, 제임스 그레고리(영어: James Gregory)는 논문 《원과 쌍곡선의 구적법에 대하여》(라틴어: Vera Circuli et Hyperbolae Quadratura)에서 함수를 다른 양들에 대한 대수 연산 및 극한 연산을 통해 얻는 양으로 정의하였다. 1665년부터, 아이작 뉴턴은 줄곧 “플루언트”(영어: fluent)라는 용어로 변수 간 관계를 지칭하였다. 1673년, 고트프리트 빌헬름 라이프니츠는 오늘날 쓰이는 용어인 “함수”(영어: function)을 곡선 위 점에 따라 변화하는 양으로 정의하였다. 1697년, 요한 베르누이는 함수를 상수와 변수가 대수 연산 및 초월 연산을 통해 구성하는 양으로 정의하였으며, 1698년에 라이프니츠의 용어를 채택하였다. 1714년, 라이프니츠는 저서 《역사》(라틴어: historia)에서 함수를 변수에 의존하는 양으로 정의하였다. 그러나, 그는 여태 미분 가능한 함수만을 다루었다.
레온하르트 오일러는 1734년에 오늘날 쓰이는 표기법 {\displaystyle f(x)}f(x)를 도입하였다. 또한, 오일러는 1748년에 저서 《무한 해석 입문》(라틴어: Introductio in Analysin Infinitorum)에서 함수를 변수와 상수로 구성된 임의의 해석적 수식으로 정의하였으며, 1775년에 저서 《미분학 입문》(라틴어: Institutiones Calculi Differentialis)에서 변수에 의존하며 그 변화에 따라 변화하는 또 다른 변수로 정의하였다.
1797년, 실베스트르 프랑수아 라크루아(프랑스어: Sylvestre-François Lacroix)는 저서 《미분과 적분에 대하여》(프랑스어: Traité du Calcul Différentiel et du Calcul Intégral)에서 수식으로 표현될 필요가 없는, 더 넓은 함수의 개념을 도입하였으며, 5차 방정식의 근이 5차 방정식의 계수의 함수라는 예시를 들었다. 1811~15년, 조제프루이 라그랑주는 저서 《역학 해석》(라틴어: Mecanique analytique)에서 “함수”라는 용어를 거의 모든 유형의 함수에서 사용하였다.
조제프 푸리에는 함수가 해석적 수식으로 표현될 수 있을 필요가 없다고 주장하였으나, 동시에 모든 함수는 푸리에 급수로 표현될 수 있다고 주장하였다. 그러나 그는 임의의 유한 구간에서 유한 개의 불연속점만을 갖는 함수만을 다루었다.
함수의 현대적 정의는 게오르크 칸토어가 제기한 집합론에 기반한 것이다. 버트런드 러셀은 집합을 기반으로 수학의 공리를 재서술하면서 함수 역시 이를 기반으로 재정의하였다.
어원
17세기 고트프리트 빌헬름 라이프니츠는 수학 저서에서 라틴어 단어 functio를 주로 ‘기능’이란 뜻으로 썼다. 이후 요한 베르누이 등이 functio를 기술적인 해석학 용어로 쓰기 시작했다. 이것이 다른 유럽 언어로 전파되었다.
영어 function의 번역어로 ‘함수(函數)’를 쓰기 시작한 사람은 이선란과 알렉산더 와일리(영어판)이다. 그들은 번역서 《대수학(代數學)》(1859)과 《대미적습급(代微積拾級)》(1859)에서 ‘함수(函數)’라는 용어를 썼다. 함(函)은 ‘상자’·‘담다’라는 뜻으로, 한 변수가 다른 변수를 담고 있다는 뜻으로 용어를 의역한 것이다.
凡此變數中函彼變數者,則此為彼之函數。
어떤 변수가 다른 한 변수를 포함한다면, 이 변수는 포함된 변수의 함수이다.
— 《대수학(代數學)》
Any expression which contains x in any way is called a function of x: thus a+x, a+bx2, &c.
x를 어떤 형태로라도 담고 있는 모든 식은 x의 함수로 부른다: a+x, a+bx2 등이 있다.
— 오거스터스 드모르간, 《The Elements of Algebra》
‘함수’가 영어 단어 function의 발음을 음역한 단어라는 설이 있지만 두 발음이 크게 달라 근거가 희박하다. 이선란은 상수·변수·계수·지수·급수 등의 번역어도 만들었지만 그 어떤 것도 음역이 아니다.