칼의 날카로운 모서리는 물체에 압력을 가하고, 그 압력을 통해 물체의 분자 간 결합을 끊어내는 역할
칼이 물질을 자르는 원리는 물질의 분자 구조를 파괴하는 것입니다. 칼의 날은 매우 날카롭고 단단하여 물질의 분자를 강하게 압축하고 파열시키는 역할을 합니다. 이 과정에서 물질의 분자가 분리되고 물질이 잘려나가게 됩니다. 이러한 원리를 이용하여 칼은 다양한 물질을 잘라낼 수 있습니다. 그리고 칼의 날이 물질을 자르는 데에 가장 적합한 각도로 설계되어 있기도 합니다. 따라서 칼은 다른 물질을 잘라내는 데에 가장 효과적인 도구 중 하나
압력의 과학, '칼'…면도날이 털에 무뎌지는 과정은?
칼을 비롯한 날붙이는 다른 물체에 닿는 면적을 최소화해 압력을 높이는 원리로 작동한다. 압력은 단위면적에 가해지는 힘으로 같은 힘이라도 더 좁은 면적에 가해지면, 압력이 커진다. '칼이 날카롭다'는 개념은 과학적으로는 단면적을 최소화해 효율적으로 압력을 높일 수 있다는 뜻에 가깝다.
이러한 칼의 절단력은 압력과 표면 재질 등과 관련이 있다. 석기시대부터 청동기, 철기로 넘어오며, 더 날카롭게 만들 수 있고 단단한 소재가 개발되며 인류가 자를 수 있는 물체의 범위도 넓어졌다. 현대에는 단단하게 만든 초경합금이나 다이아몬드 코팅을 한 칼도 제작돼 쓰이고 있다.
재질의 발전뿐 아니라 압력을 높이는 기술도 인류의 절단력을 높였다. '물 칼'이 대표적이다. 물은 단단함과 거리가 멀어 보이지만, 고압의 물을 분사하는 물 칼은 철을 절단하거나 다이아몬드 등 보석을 세공하는 데 쓰인다. 물 칼은 열 발생이 적어 물질을 거의 변화시키지 않아 정밀 세공 등에 활용된다.
칼은 가공·공예·요리·수술·위생 등 목적에 따라 다양한 소재가 개발돼 쓰이고 있고, 성능을 높이는 연구도 이뤄지고 있다.
면도날 역시 활발히 연구·개발이 이뤄지고 있는 분야 중 하나다. 면도날은 스테인리스강부터 티타늄합금에 이르기까지 다양한 합금이 쓰인다.
사람의 털은 스테인리스강의 50분의1 정도의 강도를 가지는 것으로 알려졌다. 강도가 낮은 털만 자르는 면도날이지만, 사용하다 보면 쉽게 무뎌져 날을 갈아주거나 교체를 해줘야한다. 단단하다고 알려진 각종 합금이 면도날에 쓰이는 것도 절삭력과 수명을 늘리기 위한 노력 중 하나인 셈이다.
2020년 매사추세츠 공과대학교(MIT)의 재료과학 및 공학부의 세말 셈 타산 교수 연구팀은 면도날이 무뎌지는 과정을 전자현미경을 통해 관찰해 학술지 사이언스(Science)에 발표했다.

이번 연구의 제1 저자 대학원생 지안루카 로시올리(Gianluca Roscioli)는 예비실험으로 면도 후 매번 일회용 면도기를 주사전자현미경(Scanning electron microscope)을 이용해 촬영하면서, 면도날이 어떻게 변화하는지 추적 관찰했다.
그 결과 면도날이 털의 접촉에서 발생하는 마찰 등으로 마모되는(갈려나가는) 현상은 조금 나타났다. 연구에 따르면 조그만 흠집이 먼저 생기고 그 중심으로 다른 흠집이 성장하면서 면도날이 무뎌지는 현상이 관측됐다.
즉 접촉면의 면도날 원자들이 균일하게 서서히 떨어지며 날이 무뎌지는 게 아니라, 불완전한 제작과정이나 이전의 면도에서 발생한 흠집을 중심으로 무뎌지는 셈이다.
연구팀은 면도날이 고정된 모발을 자르는 장치를 만들어 미세 흠집이 특정한 부분에서만 나타나는 현상을 분석했다. 모발 굵기에 상관없이 모발에 칼날이 수직으로 들어갈 때는 날에 흠집이 잘 생기지 않았다. 하지만 모발이 고정되지 않은 채 자유롭게 휘어진 상태에서 칼날과 비스듬하게 만날 때는 흠집이 쉽게 생기는 것이 확인됐다.
또 추가 분석을 위해 면도 상황에 대한 컴퓨터 시뮬레이션(모의실험)도 이뤄졌다. 면도날의 미세한 구조가 균일하지 않을 때 상대적으로 약한 부분에서 먼저 흠집이 생기게 되고, 그 흠집으로 주변의 구조가 균일하지 않게 돼 무뎌지는 현상이 가속됐다.
연구팀은 이 같은 내용을 바탕으로 흠집이 덜 생기도록 균일한 면도날을 만드는 공정을 개발하는 중이다.
타산 교수는 "매우 단단한 금속 등이 사람의 머리카락처럼 부드러운 것을 자를 때 미세하게 파손되는 현상은 흥미롭다"며 "시뮬레이션 결과는 면도날의 재료가 균질하지 않을 때, 가해지는 힘(응력)을 증가시켜 부드러운 털을 자를 때도 균열이 발생하는 것을 설명한다"고 말했다.
Principle #1: A knife is a wedge
You likely remember simple machines from sciences classes in school: pulleys, levers, inclined planes, etc. A wedge is a simple machine with a simple, easy to understand formula.
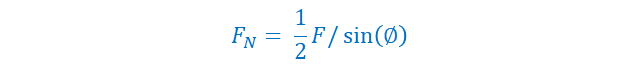
Normal force exerted by a wedge equals half the input force divided by the sine of the wedge’s angle. For a double-bevel knife, phi is degrees per side and so two normal forces will be exerted, one from each face of the knife.
Normal force points perpendicular away from the face of the wedge. For knives, it makes a little more sense to convert to lateral force (pointing perpendicular away from the center of the knife). We can use a trick of trigonometry to convert to lateral force.

Lateral force exerted by a wedge equals half the input force times the cotangent of the wedge’s angle.
A short, thick wedge in general requires more force than a long, thin wedge. But does this same principle apply to knives?
Proof #1a: A thin knife cuts better than a thick knife
This is easy to prove by calculating lateral force of two flat-ground knives as wedges. Bear in mind that lateral force is what splits apart a product as the knife passes through it, so a low lateral force means lots of pushing and cracking. So let’s compare lateral force of 7 vs 15 degrees.

A knife with 7 degrees per side pushes food apart much better than a knife with 15 degrees per side.
Proof #1b: A knife thick behind the edge will cut poorly
Of course, few knives are flat-ground from spine to edge. Most are made up of multiple bevels and we can calculate lateral force in parts as in the image below:
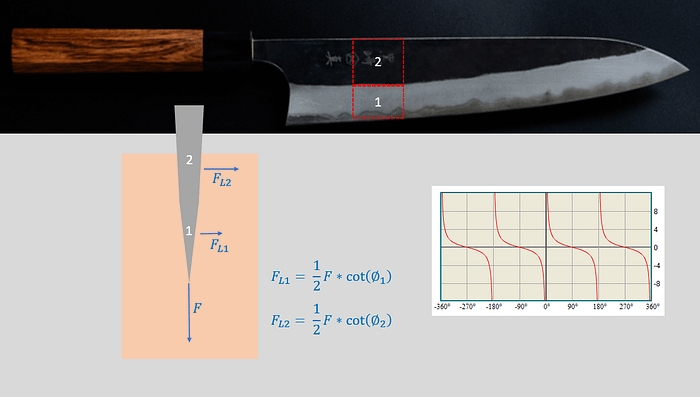
Note: F_L1 and L2 are proportions, not absolute values. Otherwise, we would double our force simply by doubling the amount of bevels. I don’t want to overcomplicate things, but the simple answer is that their true values depend on how much area of each bevel is pushing on the product.
In this case, both F_L1 and F_L2 are fairly high. The knife should cut well. What happens when F_L1 is low?

Comparing force generated by a knife thin behind the edge (left) with one thick behind the edge (right)
Notice that although thickness at the spine is equal, bevel 1 is much thicker now. In fact, because it’s so thick, F_L2 will be even greater for the knife on the right than on the left! This does not mean it will cut better though — quite the opposite. We can use our calculations from proof 1a as example values for F_L1, so imagine that the left knife has a F_L1 of around ~2 times that of the right knife.
This means that as the knife moves through the food, the actual edge bevel will struggle to separate food if that bevel is too thick — it just doesn’t generate enough force to separate the product and move further. That’s why wedging happens! In fact, F_L2 becomes so strong relative to F_L1 that it cracks the food apart like breaking a carrot in two with your hands. That is a lot of force and defeats the purpose of using a knife.
Principle #2: Flat surfaces cause sticking
Most high school courses treated friction as an acknowledged exclusion from the material, hence the ever-present “frictionless vacuum” that many homework problems took place in. For those who did discuss friction, you’ll recall that the equation looks like this:

The force of kinetic friction equals the coefficient of kinetic friction times normal force.
A quick refresher — the input force F_i pushes the object up the ramp while F_f resists that motion. The coefficient of friction (u_k) is a value that can be looked up in a table and depends on materials being used, so the most important value to determine friction is F_N or how much normal force is exerted by the object.
But what happens when an object’s surface is curved? It turns out that for convex knives, we can use the integrated form of this equation:

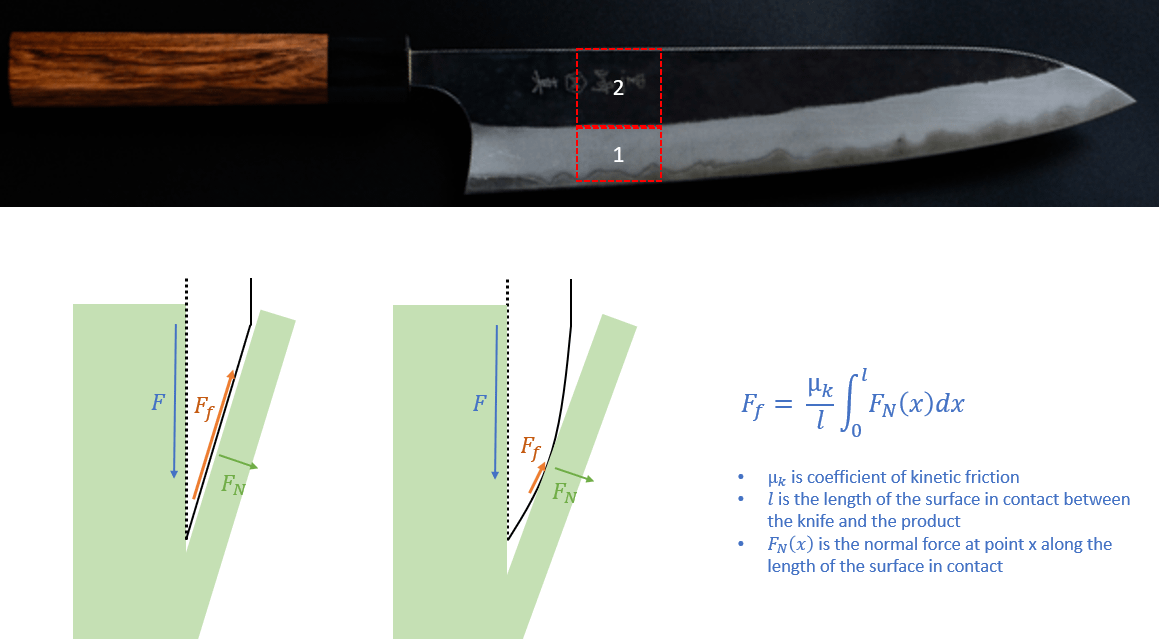
For nonuniform surfaces, the force of friction must be integrated across the entire contact surface.
Unlike ramps where gravity is the source of normal force, in knives the amount of surface area is proportional to kinetic friction. In the image above, the knife on the left will have friction dragging along the entire length of the bevel; the convex knife however only has friction in a small contact area.
In reality, of course, things we cut with knives are bendy and so a convex knife won’t result in a single point of contact like the image shows. But surfaces with less contact will exert less normal force; thus, they contribute minimal friction while allowing more efficient portions of the knife to perform work on splitting the product.
Proof #2a: A convex surface has less friction than a flat surface
The following graphs show functions of normal force of a flat and convex surface both with average angle of 14 degrees operating on an object with plastic (bendy) tensile properties
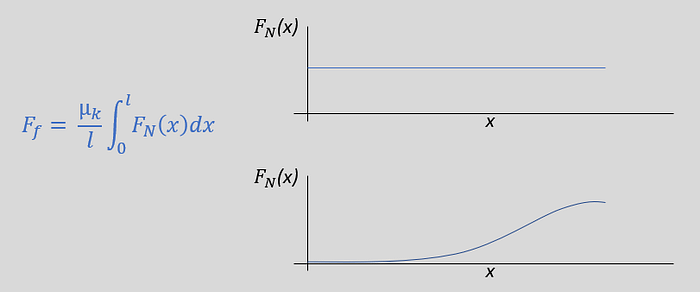
Note that both y axes are the function of normal force along the length of the blade’s grind (e.g. from edge to spine) where the knife touches the product. These graphs are to scale with one another and derived by combining the normal force equations above with plastic deformation charts taken from Wikipedia.
To understand what these graphs mean, it may be helpful to know that the integral sign in the equation to the left means we’re measuring the area under the curve. For a back-of-the-envelope calculation I did in Excel, the flat ground surface had friction four times higher than the convex surface (~2 vs. ~0.45 F_N).
Consequences
Thus far we’ve proven a few things: thin grinds cut better than thick grinds, thinness behind the edge matters a lot, and convexity reduces sticking due to friction
There’s a few hidden landmines we’ve avoided until now. I will highlight just two
- You may have caught in the last chart that plastic deformation means most force is concentrated in upper bevels, e.g. close to the spine rather than the edge. So why does thickness behind the edge matter?
- The second is that convexity and thinness are tradeoffs; that is, a very thin knife cannot have much convexity.
First, indeed because things bend, more force will be exerted near the spine than near the edge. In reality, the free body diagrams (pictures with arrows) above are an oversimplification because knives don’t cut in a single location or uniformly. To give one example, we can think of the force near the spine as a lever that actually splits the product near the edge as well. This is really what causes bad wedging — the “crack!” and sudden drop of the knife variety. Thinness behind the edge still matters.
Second, this is why there is such great debate over lasers vs. workhorse grinds. No experienced user/maker doubts that convexity and thinness are important, but exactly where the ideal ratio lies is hotly contested. I don’t have an answer for this, but for now I’ll leave you with this excellent follow-up reading from 2017: https://www.kitchenknifeforums.com/threads/a-basic-explanation-of-asymmetry.33951/