| 엔트로피 물체의 열적 상태를 나타내는 물리량의 하나로 흔히 일반인들에게 무질서도라고 알려져 있기도 하다.[1] 통계역학으로 엔트로피가 미시상태의 수에 대응된다는 것이 밝혀졌다. 엔트로피에 대해 기술한 것이 열역학 제2법칙이며, 자연현상의 물질의 상태 또는 에너지 변화의 방향을 설명해준다. '엔트로피'라는 이름은 클라우지우스-클라페이론 식으로 유명한 루돌프 클라우지우스라는 독일의 물리학자가 1865년에 붙인 것인데, '에너지'라는 말의 어원인 그리스어 ἐνέργεια(에네르게이아)에서 전치사 ἐν-(엔-)을 남기고, '일, 움직임'이라는 의미의 어간 ἔργον(에르곤) 부분을 '전환'이라는 의미의 τροπή(트로페)로 바꾸어 조합해 만든 말이다 |
열역학은 물론 열 현상을 다루는 분야이다. 일찍이 화학혁명을 주도했던 라부아지에게 열소(caloric)라는 입자개념을 도입해 열 현상을 설명하려고 했으나 결과적으로 올바른 방향은 아니었다. 근대적인 열역학의 출발점은 보통 프랑스의 사디 카르노(1769~1832)가 《화력의 원동력에 대한 고찰》을 출판한 1824년으로 잡는다. 증기기관이 등장하면서 사람들의 관심은 어떻게 하면 증기기관 같은 열기관에 똑같은 열량을 투입해서 최대한의 역학적인 일을 시킬 수 있을 것인가였다. 즉, 열기관이 등장하자 열이 어떻게 일로 바뀌는지 그 효율은 어떻게 되는지가 궁금했고 이를 연구하는 과정에서 열역학이 정립되었다. 카르노가 한 일이 바로 이것이었다. 카르노는 이상적인 열기관 모형을 만들어 높은 온도의 열원에서 투입된 열량이 어떻게 역학적인 일로 바뀌고 낮은 온도의 열원으로 열량이 빠져 나가는지를 연구했다. 이를 카르노 엔진이라 하는데 물리학 교과서에 꼭 등장하는 개념이다. 증기기관이나 현대적인 내연기관도 따지고 보면 근본적으로 카르노 엔진이라 할 수 있다. 열이 열기관 속에서 역학적인 일을 하려면 기체가 필요하다. 열을 받은 기체가 팽창하면서 예컨대 실린더 속의 피스톤을 밀어내면 그게 바로 역학적인 일이다. 증기기관에서는 수증기가 들어가고 내연기관에는 가솔린이 들어간다. 카르노 엔진에는 이상적인 기체, 즉 이상기체가 그 역할을 한다.
카르노 엔진의 열효율, 즉 투입한 열량 대비 역학적인 일을 한 비율은 두 열원의 온도비율에 의해서만 결정된다. 특히 두 열원의 온도가 유한한 이상 카르노 엔진의 열효율은 결코 1이 될 수 없다. 높은 온도에 대한 낮은 온도의 비율만큼은 버려지는 열로 빠져나갈 수밖에 없다. 카르노 엔진은 이상화된 열기관이기 때문에 실제 열기관보다도 열효율이 높다. 그럼에도 열기관이 높은 온도의 열원에서 열량을 가져와 엔진을 돌리고 낮은 온도로 열을 방출하는 이상 결코 열효율 100%를 달성할 수 없다. 열효율이 100%가 되려면 열을 가져오는 고온 열원의 온도가 무한대이거나 열이 빠져나가는 저온 열원의 온도가 절대 0도여야 한다. 이는 현실에서 불가능하다.
열역학과 관련해서는 두 가지 중요한 법칙이 있다. 제1법칙은 대략 19세기 중반에 여러 사람이 동시에 발견했다. 독일의 율리우스 로베르트 폰 마이어(1814~1878)와 헤르만 폰 헬름홀츠(1821~1894), 루돌프 클라우지우스(1822~1888), 그리고 영국의 제임스 줄(1818~1889), 윌리엄 톰슨(1824~1907) 등이 주역이다.
제1법칙을 말로 풀어서 기술하자면 어떤 물리계에 열량을 공급하면 그 물리계는 공급된 열량으로 역학적인 일을 하고 내부 에너지를 증가시킨다는 내용이다. 언뜻 당연해 보이는 이 말 속엔 중요한 두 가지 의미가 포함돼 있다. 첫째, 열이 역학적인 일 또는 에너지와 등가이다. 마이어는 열대지방에서는 사람들의 정맥피가 다른 지역에 있을 때보다 더 선홍빛을 띠는 것을 보고 열과 에너지가 등가라는 힌트를 얻었다. 라부아지에는 이미 호흡과 연소가 근본적으로 같다는 사실을 간파했었고 마이어도 이점을 알고 있었다. 열대지방에서 정맥피가 더 붉은 것은 그만큼 혈액 속에 산소가 더 많이 남아 있다는 말이고 그것은 산소를 이용한 ‘연소(호흡)’작용으로 열을 많이 낼 필요가 없기 때문이라고 마이어는 결론지었다. 열대지방에서는 체온유지에 열이 덜 소모된다. 그래도 사람 몸을 움직이려면 에너지가 필요하다. 마이어는 이런 추론 과정에서 열과 에너지가 서로 교환가능하다는 결론에 이르렀다. 열은 에너지의 또 다른 형태라는 뜻이다. 생체열을 연구하던 생리학자 헬름홀츠도 독립적으로 비슷한 결론을 얻었다.
한편 줄은 물통에 물을 담고 그 속에서 프로펠러를 돌려 물을 휘저으면 수온이 올라간다는 사실을 알아냈다. 즉 물리적인 일이 열로 바뀐 것이다. 물리적인 일(work)은 역학적인 에너지와 등가이므로 결국 줄도 에너지와 열의 등가관계를 확인한 셈이다. 그의 업적을 기려 지금도 에너지의 단위로 줄(Joule)을 쓰고 있다.
둘째, 제1법칙은 결국 에너지 보존법칙이다. 열기관에 유입된 열량, 즉 에너지는 역학적인 일(=에너지)을 하고 내부 에너지를 증가시킨다. 그러니까 에너지가 어디서 사라지거나 갑자기 생기는 일은 없다. 에너지가 보존된다는 건 너무 당연한 거 아냐? 라고 생각할지 모르겠지만 제1법칙은 열과 에너지의 전환관계를 발견하고 열 현상에 적용되는 에너지 보존법칙을 찾았다는 점에서 의의가 있다.
믿기 힘들겠지만 21세기에도 열효율이 200%가 넘는 영구기관을 발명했다는 기사가 유력 통신사를 통해 유통되고 있는 게 우리 현실이다. 열효율이 200%라면 석탄 하나를 태웠을 때 석탄 두 개를 태운 에너지가 나온다는 얘기이다. 당연히 과학의 세계에서도 언제나 기존 법칙과 패러다임을 깨뜨리는 현상이 나올 수 있다. 그러나 이미 잘 확립된 체계를 허무는 주장이 있다면 확실히 믿을만한 또는 검증 가능한 증거가 있어야 한다. 과학자들이 결과적으로는 기존 체계를 허무는 데에 어떤 거리낌이나 주저함도 없이 혁명적인 기질을 갖고 있지만 그 과정은 대단히 보수적이어서, ‘앙시앵 레짐’으로 버틸 수 있는 데까지 끝까지 버틸 수 있는, 가능한 모든 방법을 동원하는 데에도 굉장히 능숙하다. 새로운 결과를 검증하는 과정이 혹독한 것은 이 때문이다. 물론 일반인들이 그렇게까지 엄밀할 필요는 없다. 다만, 최소한의 과학적인 마인드를 가질 필요는 있다. (기자라면 더욱 그렇다.) 아마도 그 영구기관을 취재한 기자가 열역학 제1법칙을 배웠더라면 그런 기사를 내기 전에 꼼꼼하게 막전막후를 따져봤을 것이다.
그러나 열역학의 꽃은 누가 뭐래도 열역학 제2법칙이다. 흔히 줄여서 그냥 ‘제2법칙(2nd Law)’이라고 한다. 1850년 클라우지우스가 《열의 동력에 관하여》라는 논문에서 주장한 법칙이다.
제2법칙은 한마디로 말해 열은 항상 온도가 높은 곳에서 낮은 곳으로 흐른다는 것이다. 즉, 자연현상에는 방향성이 있다. 카르노 엔진의 예를 들자면 아무리 이상적인 열기관을 만들더라도 열효율이 결코 100%가 되지 않으며 어떻게든 낭비되는 열량이 있다. 그래서 카르노 엔진이 제2법칙이 나오기 전에 그 내용을 담지하고 있다고도 해석할 수 있다.
아이스 아메리카노를 만드는 과정을 생각해 보자. 먼저 컵에 얼음조각을 잔뜩 넣는다. 거기에 물을 붓고 마지막으로 에스프레소 샷을 넣는다. 얼음이 녹으면서 커피의 온도가 내려가 시원한 아메리카노를 즐길 수 있다. 이는 우리가 매일 겪는 익숙한 현상이다. 만약 이 상태에서 열이 얼음에서 물과 에스프레소로 흐르면 어떻게 될까? 얼음의 온도는 더욱 떨어지고 물과 에스프레소는 끓어 넘치는 놀라운 광경을 목격하게 될 것이다. 그렇다고 해서 에너지 보존법칙이 깨지는 것도 아니다. 무슨 이유에서인지 우리 우주에서는 그런 일이 벌어지지 않는다. 보일러로 차가운 방을 데울 수 있는 것도 제2법칙 때문이다.
제2법칙에서 중요한 개념이 엔트로피(entropy)이다. 엔트로피란 역학적인 일을 할 수 없는 열량과 관련된 양이다. 열기관이 열을 이용해 역학적인 일을 할 때 항상 낭비되는 열량이 있다. 카르노 엔진은 이상화된 기계라서 낭비되는 양이 최소량이다. 현실의 열기관이나 열현상에서는 효율이 훨씬 더 떨어진다. 즉 낭비되는 열량이 훨씬 더 많다. 엔트로피라는 양으로 번역하자면 카르노 엔진에서는 엔트로피 변화가 없지만 현실의 열기관에서는 엔트로피가 커진다. 따라서 제2법칙은 다음과 같이 (엄밀하게는 몇 가지 조건이 붙지만) 정리할 수 있다.
엔트로피는 결코 감소하지 않는다
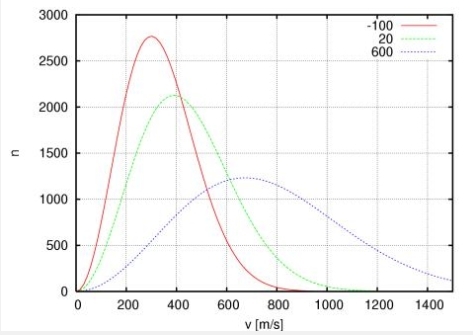
엔트로피를 좀 더 직관으로 이해하려면 열 현상을 보다 미시적인 수준에서 기술하는 방법이 있다. 온도, 부피, 압력 등은 거시적인 물리량들이다. 이를 미시적으로 다루려면 예컨대 열기관을 움직이는 기체를 미시적으로 봐야 한다. 지금은 너무나 당연하게 생각되겠지만 당시에는 기체의 운동을 분자로 이해하겠다는 발상 자체가 새로웠다. 그 일을 했던 사람이 19세기의 뉴턴이라 불리는 영국의 제임스 맥스웰(1831~1879), 그리고 오스트리아의 루트비히 볼츠만(1844~1906)이다. 기체를 구성하는 분자는 그 숫자가 굉장히 많다. 또한 서로 빠르게 충돌하면서 주어진 공간 속에서 특정한 부피를 차지하고 압력을 미친다. 보통은 이렇게 많은 개수의 입자를 다룰 때 평균값을 생각하기 마련이다. 즉, 수많은 기체분자들이 굉장히 빠른 제각각의 속도로 날아다니면서 서로 충돌할 텐데 이들 속도의 평균이 얼마인지를 따지는 것이다. 여기서 한 걸음 더 나아간 것이 맥스웰이었다. 맥스웰은 14세에 수학논문을 쓸 정도로 (주제가 아주 대단하지는 않았다지만) 수학적 재능이 탁월한 천재였다. 맥스웰은 자신의 재능을 마음껏 발휘해 기체분자의 속도에 대한 ‘분포함수’를 찾아냈다. 분포함수란 예를 들면 시험에서 0점 받은 학생이 몇 명, 10점 받은 학생이 몇 명, ..., 100점 받은 학생이 몇 명 하는 식으로 어떤 변수(기체분자의 속도)에 대해 몇 개가 분포하는지를 나타내는 함수이다. 그러니까 속도가 얼마인 분자가 몇 개인지를 확률적으로 알려주는 함수를 찾은 것이다. 그 분포함수는 비교적 익숙한 형태의 함수로, 분자의 속력(속도의 크기)에 대한 정규분포함수(또는 가우스 함수)였다. 볼츠만은 맥스웰의 성과를 발전시켜 볼츠만의 분포함수가 일반적인 에너지를 가진 경우로 확장시켰다. 이 결과를 맥스웰-볼츠만 분포라 부른다.
기체의 열 현상을 이해하기 위해 기체를 구성하는 수많은 미시적인 분자를 도입하면 개별 입자의 움직임을 동역학적으로 기술하기란 (원리적으로 뉴턴역학을 적용할 수 있음에도 불구하고) 사실상 불가능하다. 맥스웰과 볼츠만은 이들을 통계적으로 다루는 방법을 정립함으로써 거시적인 열 현상을 미시적인 입자들의 통계역학으로 환원하는 데에 성공했다. 이는 통계역학의 새 시대를 열었을 뿐만 아니라 분자와 원자의 존재를 강력하게 뒷받침하게 되었다.
한편 미국에서는 조시아 윌라드 깁스(1839~1903)가 통계적인 방법을 도입해 열 현상을 연구하고 있었다. '통계역학'이라는 말을 처음 도입한 것도 깁스였다. 깁스는 화학퍼텐셜이라는 개념을 도입해 화학반응도 물리적인 통계역학으로 설명할 수 있는 길을 열었다.
이런 미시적인 관점에서 엔트로피를 새롭게 정의한 사람은 볼츠만이었다. 볼츠만에 따르면 엔트로피는 어떤 계가 취할 수 있는 미시적인 상태의 수로 결정된다(1877년). 구체적으로는 그 상태의 수의 로그값에 비례한다. 비례상수는 물론 볼츠만 상수이다. 정성적으로 말해 미시적인 상태의 수가 증가하면 엔트로피가 커진다. 간단한 예를 들어보자. 맑은 물이 담긴 통에 잉크 한 방울을 떨어뜨리면 시간이 한참 지난 뒤 전체 물이 흐려진다. 이는 잉크를 구성하는 분자가 물통 전체에 골고루 퍼지기 때문이다. 잉크 분자들이 조그만 잉크 방울 속에 몰려 있을 경우의 수와 넓은 물통에 골고루 퍼져 있을 경우의 수를 따져 보면 엄밀하게 계산해 보지 않더라도 전자의 경우의 수가 훨씬 더 작음을 알 수 있다. 따라서 잉크 분자가 조그만 방울로 몰려 있을 때 엔트로피가 낮다. 제2법칙에 따르면 방울로 모여 있던 잉크분자가 물 전체로 퍼져나가는 현상은 가능해도 물 전체에 퍼져 있던 잉크분자가 다시 방울로 모이진 않는다. 이는 우리의 일상경험과도 일치한다. 비빔밥을 먹을 때도 마찬가지이다. 처음에 비빔밥을 받으면 갖은 나물과 고기와 밥이 잘 정돈돼 있다. 이걸 숟가락으로 휘저으면 밥과 나물과 고기와 양념이 골고루 잘 섞인다. 한번 섞인 비빔밥을 아무리 계속 휘저어도 원래 나물과 고기와 밥으로 다시 나누어지지 않는다. 얼음과 물과 에스프레소가 모여 아이스 아메리카노가 되는 과정도 이와 비슷하다. 이것이 열역학 제2법칙이다.
존재할 수 있는 경우의 수가 적다는 것은 쉽게 말해 한쪽에 쏠려 있다는 뜻이고 이는 일상 용어로 ‘질서정연하다’고 말할 수 있다. 즉, 엔트로피가 낮다는 말은 경우의 수가 작다는 뜻이고 이는 질서가 잡혀 있다, 또는 무질서도가 낮다는 말이다. 따라서 엔트로피를 흔히 ‘무질서도’라고도 부른다. 그렇다면 제2법칙은 자연의 무질서도가 증가하는 법칙이라고 말할 수 있다.
부분적으로는 엔트로피가 감소하는 경우도 있다. 냉장고가 대표적이다. 냉장고 안은 차갑게 유지되고 냉장고 밖의 열판은 더워진다. 이렇게만 놓고 보면 온도가 낮은 데서 높은 곳으로 열이 흐르는 것처럼 보인다. 이는 제2법칙에 어긋나게 엔트로피가 낮아지는 것처럼 보인다. 그러나 냉장고에서 중요한 요소는 모터가 전기에너지를 받아 ‘물리적인 일’을 한다는 점이다. 모터가 냉매를 압축하고 팽창시키는 순환과정을 돌리지 않으면 냉장고가 작동하지 않는다. 모터와 전기에너지를 모두 포함시키면 당연히 전체 엔트로피는 증가한다. 제2법칙은 고립된 계(isolated system)에 적용되는 법칙이다.
엔트로피가 낮아진다는 것은 질서가 높아진다는 뜻이다. 일을 해서 엔트로피를 낮춰 질서를 높이는 경우를 우리는 일상에서 흔히 경험한다. 어질러진 책상은 무질서도, 즉 엔트로피가 높다. 책상을 질서 있게, 즉 엔트로피가 낮은 상태로 정리하려면 우리가 몸을 움직여 ‘일’을 해야 한다.
기체분자운동론과 열역학 법칙들의 확립은 19세기 과학의 중요한 성취들이다. 그 속에는 암묵적으로 분자와 원자의 존재가 내포돼 있다. 화학에서 이미 아보가드로의 법칙이 분자의 존재를 예견했듯이 이쯤 되면 19세기에 분자와 원자의 존재가 학계에 널리 받아들여졌을 법한데, 현실은 정반대였다. 19세기 후반으로 갈수록 경험주의와 논리 실증주의가 득세하게 되는데, 이들의 주요 논리는 인간의 감각경험으로 확인할 수 없는 부분은 과학적 연구의 대상이 되어서는 안 된다는 것이었다. 따라서 분자나 원자 따위를 인정할 리가 없었다. 기껏해야 수학적 또는 기술적 보조수단 정도로만 인식할 뿐이었다. 에른스트 마흐와 빌헬름 오스트발트 등이 이런 흐름을 주도했다. 학계에 영향력이 크지 않았던 볼츠만은 분자론에 대한 주류 학계의 부정적인 태도에 큰 좌절을 느꼈다. 원자와 분자의 존재에 쐐기를 박은 것은 1905년의 아인슈타인이었다. 돌턴이 근대적인 원자론을 들고 나온 지 거의 100년이 지난 시점이다.

볼츠만(Ludwig Boltzmann)
1844~1906 오스트리아의 물리학자. 특히 기체론(氣體論)의 연구로 알려졌으며, 통계역학의 기초를 쌓은 사람으로 유명하다.
황실(皇室) 재무서기관의 아들로 빈에서 태어나 빈 대학에서 물리학을 공부하면서 J. 슈테판 등과 가까이 지냈다.
1866년 빈 대학을 졸업한 후 슈테판 밑에서 조수가 되었고 67년에 학위를 취득했다.
이듬해 그라츠 대학 교수가 되었으며 그 후 한때 하이텔 베르크의 R. W. 분젠과 쾨니히스베르거, 베를린의 G. R. 키르히호프와 H. 헬름홀츠 밑에서 객원으로 지냈으나 73년 빈 대학을 비롯하여 그라츠 · 뮌헨 · 라이프치히 대학의 교수로 있었다.
그는 매우 해박했으며 처음에 그라츠에서는 수리(數理)물리학, 후에는 실험물리학 강좌를 맡았고, 뮌헨에서는 이론물리학을 빈에서는 물리학 외에 철학 강의도 했다.
그의 강의는「수정처럼 명석했다」고 한다.
그의 연구는 매우 광범위하여 이론물리학, 특히 고전역학(古典力學)과 원자론적 관점에서의 열이론의 전개와 추진이었다.
J. C. 맥스웰이 개척한 기체분자 운동론을 발전시켜 열평형상태에서 맥스웰 분포가 실현되는데 대한 엄밀한 역학적 증명에 노력하여 분포함수의 시간적 변화를 주는 볼츠만 방정식을 세웠다.
이로써 이른바 맥스웰-볼츠만 분포의 기초가 확립되었으나 다시 이것을 단서로 열현상의 불가역성(不可逆性)의 역학적 증명을 추구하여 마침내 H정리(定理) 를 제시함으로써 비가역성을 증명했다(1872).
그리고 이와 관련하여 가역성의 반론(J. 로슈미트)과 재귀성(再歸性)의 반론(E 체르멜로) 등 엄밀한 곤란이 지적되자 거기에 대답하기 위해 H정리의 물리적 의미를 탐구하여 이윽고 엔트로피의 증대는 단순한 역학적 법칙이 아니라 확률적 법칙이라는 해석에 도달하여 그 확률적 의미를 밝히는 동시에 엔트로피를 상태확률의 함수로 정의했다(1877).
유명한 S=klog W(S는 엔트로피, W는 상태확률, k는 볼츠만상수)의 식이 그것이다.
이 식의 근저에는 계(系)의 미시적(微視的) 상태가 모두 같은 선험적 확률을 가진다고 하는 가정이 있다.
그리고 이것은 그 배후로서 이른바 에르고드 가설(假說 ; 임의의 위상궤도는 에너지가 일정한 면 위의 모든 점을 통과한다고 하는 가설)과 밀접하게 연관되어 있다.
71년에 볼츠만이 도입한 이 가설은 통계역학의 성립에 중요한 공헌을 했다.
그리고 이런 결과를 점성(粘性) · 확산 등의 구체적 문제에 적용하는 면에서도 그는 정력적으로 연구 활동을 벌였다.
다른 분야에서도 맥스웰 전자기학의 검토, 유전율(誘電率)과 투자율(透磁率)의 측정에 의한 전파속도의 체크, 탄성여효(彈性餘效)의 연구 등 이 있고 특히 복사에너지의 온도 의존성(4승에 비례)의 이론적 도출(슈테판-볼츠만의 법칙)이 중요하다.
이것은 이윽고 열복사론(熱輻射論)을 전개하는데 큰 역할을 하게 되었다.
방법론적으로는 원자론의 입장을 추진 · 옹호한 것으로도 유명하며 당시 매우 성했던 에네르게티크(Energetik)의 사람들(대표자로는 E. 마하, F. W. 오스트발트, P. 뒤엠, 헬륨 등)과 논쟁을 벌였다.
에네르게티크는 실증주의 철학을 배경으로 현상론적(現象論的) 기술을 자연과학의 과제로 간주하고 그러기 위해서는 에너지를 보편개념으로 사용해야 한다고 주장하여「가상적」인 원자, 따라서 그것에 기초를 두는 기초운동론에 대한 격렬한 논란이 있었다.
특히 95년의 뤼베크 회의에서의 논쟁은 유명하다.
볼츠만은 원자론의 입장을 철저하게 옹호하여 「최후의 원자론자」라고까지 불렸다.
이 논쟁을 통해 볼츠만이 말한 「에너지에도 원자가 있을 수 있다」는 말은 후일 에너지의 양자화(量子化)를 암시한 선견지명이었다고도 한다.
만년에는 신경증에 시달리다가 1906년 목숨을 끊었다.