● 허수 (The square root of minus one; imaginary number: 르네 데카르트 그리고 레온하르트 오일러 1637, 1750)
허수는 현대에서 없어서는 안될 숫자 중 하나로 수의 개념을 확장시킨 존재이다. 적분을 고안해낸 두 천재 중 하나인 라이프니츠는 허수에 관해서 ‘존재와 비존재 사이에 있는 존재로 마치 양서류 같은 존재’라고 표현하며 성스럽고 놀라운 영혼의 피난처라고 덧붙인 바 있다. 도대체 허수는 무엇이길래 이토록 미묘한 표현을 썼을까? 허수는 제곱을 해서 -1되는 수를 일컫는다. 실수(real number)를 제곱하면 0 또는 양수가 나오는데 제곱해서 -1이 된다니 이건 보통의 숫자와 달라도 뭔가 한참 다르다.
허수의 역사는 사실 매우 오래되었다. 고대 그리스의 기하학자 헤론에 의해서 처음 개념이 잡힌 후로 1572년 이탈리아의 수학자 라파엘 봄벨비의 선형대수학 저서에서 허수의 중요성이 처음 인식되었다. 이후 데카르트 철학서 방법사설(Discours de la méthode)의 부록 기하(La Géométrie)부분에서 ‘허수(imaginary numbers)’라는 개념이 정착되었고, 오일러에 의해서 허수 단위 기호로 i가 도입되었다. 현대 수학에서는 실수(제곱하면 0보다 커지는 부분)와 허수(제곱하면 0보다 작아지는 부분)를 합쳐서 복소수(complex number)라고 부른다. 제곱해서 0보다 작아지려면 제곱해서 -1이 되는 숫자가 필요하므로 복소수를 적당한 두 실수 a와 b에 대해서 a+bi 꼴로 나타내곤 한다.
허수는 숫자 자체로도 매우 신비롭지만, 이의 기하학적 의미는 수학을 완전히 뒤바꿔놓았다고 해도 과언이 아니다. 허수가 탄생하기 전까지 모든 숫자들은 수평으로 뉘어진 직선 위에 존재하고 있었다. 하지만 제곱해서 -1이 되는 수는 직선 위에 자리 잡을 수 없기에, 영국의 수학자 존 월리스 (John Wallis)는 이를 기하학적으로 나타내고자 평면에서 수직 방향으로 공간을 넓히는 놀라운 사고의 전환을 고안해 냈다. 이후 노르웨이-덴마크의 수학자 카스파르 베셀(Caspar Wessel)이 복소수를 직교좌표에 나타내게 되었다. 즉, 직교좌표계에 한점 Z (x, y) 가 있다고 가정했을시 이는 z = x+yi 로 나타낼 수 있게 되었고, 따라서 좌표와 복소수는 1대1 대응을 이룰 수 있게 된다. 이를 통해서 허수는 마침내 숫자로 인정 받게 되었고, 가우스는 이를 이용하여 훗날 허수를 이용하여 방정식 해에 관한 일관된 규칙을 발견하게 된다.
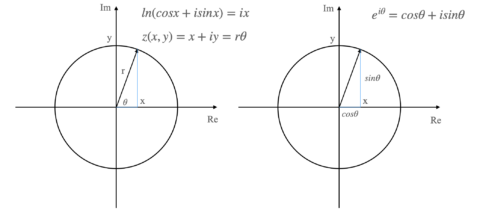
점 Z는 원점에서부터의 반지름과 각도를 이용하여 극좌표에서도 표현될 수 있는데 (z = x + yi = rθ), 이는 결국 임의의 원이 있다고 가정했을시 복소수와 삼각함수와의 관계까지 확장될 수 있게 된다. 영국의 수학자 로저 코츠(Roger Cotes)와 레온하르트 오일러(Leonhard Euler)는 복소수가 자연로그와 삼각함수 및 지수함수와의 관계식으로 표현될 수 있다는 점을 발견했다. 즉, ln(cos x + i sin x) = ix를 지수함수로 변형하여 자연로그의 밑에 ix 승은 cos x + i sin x 와 같다는 공식을 발견하게 되었는데, 이는 세상에서 가장 아름다운 공식으로 불리는 오일러의 공식이다.
허수의 중요성이 강조되는 것은 현대 물리학이 양자역학을 토대로 설명되기 때문이다. 관측 가능한 세계는 실수로 설명할 수 있지만, 양자 세계를 설명할 때는 허수가 등장한다. 대표적으로 양자역학의 기초를 이루는 슈뢰딩거 (Erwin Schr dinger) 방정식에도 허수가 등장하며 방정식의 해 역시 복소수로 나타내어진다. 허수의 장점은 불가능해 보이는 문제를 비교적 간단하게 해결해준다는 점이다. 전자전기공학에서는 허수가 없어서는 안 될 요소이며 복소수의 도움 없이는 미분방정식의 풀이가 거의 불가능하다.
또한 복소수 세계의 적분인 복소적분에서 적분 해는 실수만으로는 표현 불가능하다. 이외에도 열역학, 유체역학, 기체공학 등 수많은 분야에서 복소수가 쓰이고 있으며 신호 분석 등에서도 복소수가 쓰인다. 이처럼 허수는 과거 사고방식을 완전히 바꿔놓은 숫자이며 현대 수학과 물리학에서 가장 근본이 되는 요소 중 하나라고 해도 과언이 아니다. 현대 물리학의 혜택을 받는 우리 역시 허수의 혜택을 받고 있다.
● 오일러의 다면체 공식 (Euler’s Formula for Polyhedra: 오일러 1751)
정다각형(Regular polygon)은 모든 각의 크기와 변의 길이가 같은 다각형을 말한다. 정다각형은 변의 길이가 늘어날수록 원에 근접하는 모양을 갖게 된다. 이에 반면 정다면체 (Platonic solid)는 모든 면이 합동인 정다각형으로 이루어져 있는, 즉, 각 꼭짓점에서 만나는 면의 개수가 같은 도형을 말한다. 특이한 점은 정다면체가 다섯 가지 밖에 없다는 점이다.
이유는 알고 보면 간단하다. 정다면체가 되려면 각 면이 모두 합동인 정다각형이어야 하고, 꼭짓점에 모인 면의 개수가 모두 같아야 한다. 또한 입체도형을 만들기 위한 꼭짓점에 모이는 최소 면의 숫자는 3개이다. 먼저 각 면이 정삼각형인 정다면체는 정사면체 (정삼각형이 3개), 정팔면체 (정삼각형이 4개), 정이십면체 (정삼각형이 5개)까지만 가능하다. 정삼각형이 6개 이상 모이면 모인 각의 크기 합이 360도를 넘어서기 때문이다.
각 면이 정사각형인 정다면체는 단 한 가지 정육면체 (정사각형이 3개)뿐이다. 각 면이 정오각형인 정다면체는 정십이면체(정오각형이 3개)가 가능하다. 정오각형이 4개 이상이면 역시 모인 크기 합이 360도를 넘어선다. 정육각형은 한 각이 120도기에 3개가 모이면 360도가 되어서 다면체를 만들 수 없다. 결론적으로 정다면체는 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체로 총 다섯 가지뿐이다.
오일러는 임의의 다면체를 구성하는 점, 선, 그리고 면이 가지는 관계를 밝혀냈는데, 이는 점의 개수(V)에서 선의 개수(E)를 뺀 값에 면의 개수(F)를 더 할 경우에 나오는 값이 일정하다는 정리(V – E + F = 2)이다.
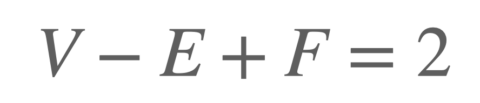

여러 특수한 다면체들은 기존의 정다면체와 유사한 모습을 지녔어도 오일러 공식이 성립하지 않는 경우가 있다. 이는 위상 관점에서 중요한 예시가 될 수 있는데, 겉모습이 비슷한 다면체가 다른 성질을 가질 수 있기 때문이다. 오일러 다면체 공식은 이어진 연구에서 정다면체가 아닌 더 복잡한 형태의 도형에서는 V – E + F가 2가 아닌 다른 값이 나올 수 있음이 확인되었고, 위 값을 오일러 표수(Euler Characteristic)라고 부르게 되었다.
따라서 다른 오일러 표수는 도형이 근본적으로 다른 성격을 띠고 있음이 밝혀진 셈이다. 오일러의 다면체 공식은 위상 수학의 기초가 되었으며 훗날 네트워크 연구로 일반화되면서 수학자들에게 더 높은 차원의 도형 연구에 큰 도움을 주었다.
● 정규분포 (Normal distribution: 가우스 1810)
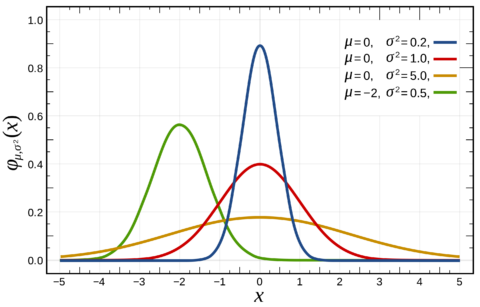
정규분포(Normal distribution 또는 가우스 분포 Gaussian distribution)는 통계학에서 가장 대표적인 연속 확률 분포 중 하나이다. 정규 분포는 평균 μ과 표준편차 σ에 의해서 모양이 결정되며, 이때의 분포를 N (μ, σ제곱)이라고 표기한다. 특히 평균 μ이 0이며 표준편차 σ가 1인 정규 분포를 표준분포(standard normal distribution)라고 부른다. 정규분포는 데이터 분포를 근사하는데 매우 자주 이용된다.
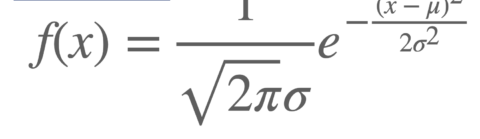
코로나 19를 거치고 국민들의 정치에 대한 관심이 정점에 다다른 요즈음, 통계는 이제 우리 생활에서 떼려야 뗄 수가 없는 존재가 되었다. 코로나 통계, 각종 여론 조사, 그리고 수능 등급 컷 예측 등에도 정규분포가 매우 다양하게 이용되고 있다. 특히, 전체 집단(모집단)에 관해서 전수 조사는 거의 불가능하기에 일정 표본만 조사함으로써 적은 시간과 비용만으로 (일정한 신뢰도를 바탕으로) 모집단에 관한 정보를 추정할 수 있는데, 이는 모집단이 정규분포를 따르면 표본 평균도 정규 분포를 따르기 때문이다.
또한 모집단이 정규분포를 따르지 않더라도 데이터가 충분히 많다고 가정할 시 위 정리가 유사하게 성립되곤 한다 (중심 극한 정리 Central limit theorem). 즉, 모집단의 평균, 분산 등을 모르더라도, 표본 집단을 대상으로 표본 평균과 분산 등만 알게 된다면 모집단에 관한 여러 추정을 할 수 있다는 점이다. 많은 통계 자료들은 정규 분포를 따르며 데이터가 정규 분포를 따른다는 가정만으로 우리가 매우 다양한 통계 분석을 수행할 수 있다는 점은 정규 분포의 큰 장점이라고 할 수 있다. 또한 이항분포, 카이제곱 분포 등 다른 확률 분포들과도 서로 밀접한 관련이 있기 때문에 정규 분포는 그야말로 통계학에서 뿌리와 같은 존재라고 할 수 있다.
● 파동방정식 (Wave Equation: 달랑베르 1746)]
파동방정식(Wave Equation)은 음파, 전자기파, 수면파 등의 일반적인 파동을 다루기 위해 사용되는 2차 편미분 방정식이다 (슈뢰딩거의 파동방정식과는 다름). 이는 라플라스 방정식의 변형으로 줄의 떨림, 얇은 판의 진동 등 자연계에서 나타나는 여러 파동 현상을 설명할 수 있다. 파동 방정식의 표현은 다음과 같다.
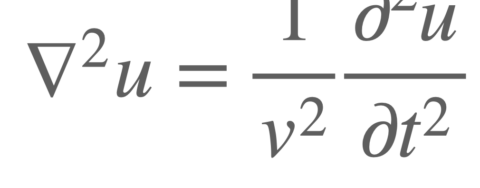
u는 파동의 진폭 파형을 나타내는 물리량으로 주로 음향파, 물결파, 지진파, 진동하는 끈의 변위 파동, 전류파, 전압 파 혹은 전자기파의 전계 혹은 자계에 해당하는 물리량이며 스칼라 또는 벡터일 수 있다. v는 전파되는 파동의 속도를 나타내며 주로 음파의 속도 (음속), 빛의 속도 (광속), 혹은 탄성 줄을 따라서 전파하는 속도 등을 나타낸다. ∇제곱은 라플라시안(Laplacian Operator)으로 공간 좌표에 관한 2계 미분 연산자를 나타낸다.
한편 특정 파동을 묘사하기 위해서는 초기 조건(initial condition)과 경계 조건 (boundary condition)등이 주어져야 한다. 위 파동방정식의 해가 어떤 함수라면 그 함수는 그에 따른 파동을 나타내며 이를 파동 함수(wave function)라고 표현한다. 파동방정식의 응용은 무궁무진하다. 우리는 음악 등의 소리, 실생활에서 가장 중요한 빛, 지진 등의 파동 속에서 살고 있기 때문이다. 파동방정식은 자유 공간상의 전자기파 파동 방정식, 전압파, 전류파 파동 방정식 등에도 쓰이며 여러 중요한 방정식의 모태가 되었다. 그중 가장 중요한 발견으로 맥스웰의 업적을 들 수 있는데, 맥스웰은 그의 방정식들에 대한 몇 가지 간단한 조작 끝에 파동방정식으로 유도하는데 성공하였고, 이에 따라서 빛이 반드시 전자기파일 것이라고 유추한 바 있다.