퍼지 이론, Fuzzy Theory

퍼지 논리(fuzzy logic)는 불분명한 상태, 모호한 상태를 참 혹은 거짓의 이진 논리에서 벗어난 다치성으로 표현하는 논리 개념이다. 퍼지 논리는 근사치나 주관적 값을 사용하는 규칙들을 생성함으로써 부정확함을 표현할 수 있는 규칙 기반기술(rule-based technology)이다.

 

퍼지 이론(Fuzzy Theory)

퍼지(Fuzzy)란 영영 사전을 찾아보면 다음과 같이 '애매 모호한' 이라는 뜻을 가지고 있다.

 

 

우리의 일상은 애매모함으로 점철되어 있다. 예를 들어, '저 남자 늘씬하고 멋지다. 저 여자 정말 예쁘다. 쌀 한 움큼. 물이 미지근하다. 오늘 날씨가 쌀쌀하다' 등과 같이 말이다. 이처럼 불완전하고, 부정확한 자료를 처리하기 위해 신경회로망을 사용하기도 한다. 여기에 퍼지 논리(Fuzzy Logic)를 추가하면 또 다른 애매모호한 것에 대한 처리의 상승효과가 가능하다. 

= 퍼지 논리(Fuzzy Logic)이란, 퍼지 이론의 특정한 명시를 이해하고 조정하기 위한 수학적 기술로서 Linguistic variable을 다루기 위한 수학적인 도구를 제공하기 위함이다. 

 

 

 

퍼지 이론은 확률 이론과는 다르다

= 퍼지 멤버쉽(Fuzzy Membership)과 확률의 값은 0~1 사이의 값을 가짐.

= 확률의 1은 어떤 사건이 일어날 확실성을 나타냄.

= 애매모호함(Fuzziness)의 1은 특정 집합에 속하는 대상에 관한 확실성(Fuzzy Set은 경계가 날카롭지 못한 집합)

예) 잘생긴 남자라는 집합이 있으면 1의 값은 그 남자가 잘생긴 남자라는 집합에 속해 있다는...

 

= 주장(assertion) x의 진리도를 [0,1] 사이의 실수로 표시(Jan Lukasiewicz)

 

 

 

퍼지 이론은 다음과 같다

= 퍼지 이론에서의 Union(합집합)과 Intersection(교집합)

: Union은 두 개중 더 큰 것             

: Intersection은 두 개중 더 작은 것     

 

예) 두 개의 Fuzzy Vector가 다음과 같이 정의되면,

A = 0    .3    .7    .4    .8            B = .8    .2    .6    .7    .9

(1) Fuzzy OR(The union of the vectors)

 = .8    .3    .7    .7    .9

(2) Fuzzy AND(The intersection of the vectors)

 = 0    .2    .6    .4    .8

 

= Fuzzy vector의 보수(Complement)

 

: 

 

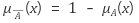
예) 위의 A 벡터에서 A의 보수는    1    .7    .3    .6    .2

= 따라서, Intersection(A, A')가 0이거나 Union(A, A')가 1이 되는 것이 아님

= 지배된 멤버쉽(Dominated Membership)은 퍼지 집합 A의 모든 요소가 퍼지 집합 B의 대응되는 요소와 같거나 적을 때를 말한다.

예) A = .1 .3 .4        B = .1 .2 .3 .4 

= 'Bart Kosko'는 Fuzzy Vector의 Cardinality(크기)와 Subsetness(부분집합 정도)를 정의

: Cardinality(크기)는 요소(element)들의 합으로 정의.

예) 3차원 벡터 Z = .3 .9 .2 일 때, Cardinality M of Z = 1.4

 

: Subsetness(부분집합 정도)는 다음과 같이 정의

예) A = 0    .3    .7    .4    .8            B = .8    .2    .6    .7    .9

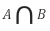
 = 0    .2    .6    .4    .8

M(A) = 2.2    M(B) = 3.2    M(

) = 2.0

 

따라서, A가 B의 부분집합인 정도 S(A,B) = 2.0/2.2 = 0.909이며 B가 A의 부분집합인 정도 S(B, A) = 2.0/3.2 = 0.625

 

 

 

 

  퍼지 이론을 적용한 하이브리드 학습 시스템(Hybrid Learning System)

역전파(Backpropagation)에서의 문제는 적절한 학습률을 선택하기가 어렵다는 것이다. 따라서 학습을 조금 더 잘 조절하여 수렴을 더 잘하기 위해 퍼지 이론을 추가한 하이브리드 학습 시스템을 이용한다. 퍼지 이론이 추가된 역전파(Backpropagation)의 학습은 'Fuzzy Logic Controller'가 추가된 다음의 구조를 따른다.

여기서 Fuzzy Logic Controller는

= Backpropagation 학습을 가지는 다층 퍼셉트론(Perceptron)의 학습 파라미터를 알맞게 하기 위해 사용

= 학습 과정의 수렴율을 개선시키기 위해 사용

= Backpropagation 알고리즘의 unknown learning parameter들의 인간언어적 서술을 도움

예) 역전파 알고리즘이 수렴하지 않을 때, "학습률을 '조금' 낮춰봐라" 라고 말할 수 있는데, 여기서 '조금'이라는 말 자체가 퍼지한 말이기 때문에 이것을 처리하기 위해 퍼지 이론을 적용

 

= Fuzzy Logic Controller의 구성은 다음과 같다

(1) Fuzzification Interface: 입력변수의 값의 범위를 일치하는 논의 영역(Universe of discourse)로 변화시키는 Scale Mapping 작업을 담당

** 여기서 논의 영역이란, 쉽게 말하면 위와 같은 퍼지 시스템의 입력데이터로 간주될 수 있는 가능한 모든 데이터에 대한 집합(영역)이라 보면 된다. 즉, 위의 Scale Mapping 작업이란, Nonfuzzy(crisp)한 입력 데이터를 적절한 언어적 값으로 바꾸는 Fuzzification 작업을 한다는 것이다. 

예) 0.33이라는 값이 입력데이터로 들어오면 이 값은 '조금 작은 값' 이라는 적절한 언어적 값으로 바꿔줌

 

(2) Fuzzy Rule Base: IF-THEN 형태로 쓰여진 언어적 제어 규칙의 집합

 

(3) Fuzzy Inference Machine: Fuzzified Input과 Fuzzy Rule로부터 규칙을 채택하는 의사 결정 논리(Decision-Making Logic)

예) IF temperature is very high, THEN set fan speed very high

와 같이 temperature가 very high라는 fuzzified input과 IF-THEN 규칙으로부터 fan speed를 very high로 세팅하는 규칙(fuzzy control action)을 채택한다.

 

(4) Defuzzication Interface: 출력변수값의 범위로 일치되는 논의 영역(Universe of Discourse)로 바꾸는 Scale Mapping 작업을 진행. 즉, 위의 3단계에서 추론된 fuzzy control action으로 부터 nonfuzzy(crisp) control action을 내는 defuzzication을 진행한다.

**여기서 output data(crisp)는 가능한 분포내에서 중심으로 정의되는 데이터로 생성(Centroid Method)

 

 

 

위와 같은 내용을 토대로 역전파(Back-propagation) 알고리즘 학습의 Fuzzy Control의 주된 아이디어는 알고리즘의 수렴속도를 빠르게 하기 위해서 Fuzzy IF-Then Rule의 형태로 "Heuristic"을 구현하는 것이다. 여기서 Heuristic은 Sum of Squared Error의 E에 의해 조정된다.

예를 들어 다음과 같이 Heuristic을 정의해보자.

(1) CE(Change of Error)를 error surface의 gradient의 근사치라고 하자.

**Error Surface는 신경망에서 n개의 가중치(weight)가 주어졌을 때, 이 가중치에 대한 에러값을 plotting하여 얻은 n차원의 landscape 함수라고 보면 될 듯 하다...

(자세한 내용은 https://www.byclb.com/TR/Tutorials/neural_networks/ch10_1.htm를 참조)

예를 들면, E(n-2) = 0.34    E(n-1) = 0.32    E(n) = 0.33이라면, 

n-1과 n-2 사이의 CE값은 0.32 - 0.34 = -0.02

n과 n-1 사이의 CE값은 0.33 - 0.32 = 0.01

(2) CCE(change of CE)를 수렴의 가속도에 관련된 second-order gradient의 근사치라고 하자.

**쉽게 말하면 위의 예에서 CCE는 두개의 CE의 차이 값인 0.01-(-0.02) = 0.03

(3) Rule Base는 다음과 같이 정한다

1) IF 알고리즘의 여러 연속적인 반복에서 CE가 부호변화가 없는 작은 값이라면, THEN 학습율 변수의 값이 증가되어야만 함

**즉, CE의 값이 계속 (+)이거나 계속 (-)일때는 학습율 변수가 작다고 판단한다는 것이다.

2) IF 알고리즘의 여러 연속적인 반복에서 CE의 부호변화가 일어나면, THEN CCE 값에 관계없이 학습률 파라미터(Learning-rate parameter)의 값이 감소되어야 함

**위의 IF는 Error가 계속 진동되고 있다는 말이므로 학습률이 너무 크다는 뜻

3) IF 알고리즘의 연속적 반복에서 부호변화가 없고 CE와 CCE 둘다 작은 값이라면, THEN 학습률 파라미터의 값과 Momentum Constant값 둘다 증가되어야 함

**대체로 CE가 계속 (-)이면 CCE는 (+)이고, CE가 계속 (+)이면 CCE는 (-)인 경향이 있음을 활용

위의 (1)~(3)의 3가지 Rule을 보면 Error Surface에서의 Gradient의 부호변화는 CE의 부호변화와 동일하다.

 

그러면 마지막으로 위의 Heuristic을 이용하여 다음과 같이 학습률 파라미터(learning-rate parameter)의 퍼지 로직 제어를 위한 결정표(Decision Table 또는 Rule Base of Fuzzy Supervisor)을 만들 수 있다.

CCE	CE
	NB	NS	ZE	PS	PB
NB	NS	NS	NS	NS	NS
NS	NS	ZE	PS	ZE	NS
ZE	ZE	PS	PS	PS	ZE
PS	NS	ZE	PS	ZE	NS
PB	NS	NS	NS	NS	NS

(NB: Negative Big, NS: Negative Small, ZE: Zero, PS: Positive Small, PB: Positive Big)

(각각의 경우에 따라 자기가 임의로 구간을 정의해줘야 함. 예를 들면 NB는 학습률이 -0.1~-0.01 이라는 구간이고 NS는 ~0.01~0이라는 구간이고..)

 

예를 들어 위에서 Heuristic을 토대로 CE와 CCE가 각각 ZE, NS 였다면, 학습률 파라미터를 '조금 증가'시켜주는 것이다.

 

위의 테이블과 같이 Momentum Constan에 해당하는 테이블을 만들 수 있을 것이다. 또한, 이 테이블은 아무나 만들어서는 신뢰도가 떨어지고, 실제로 많이 학습시켜봤던 전문가들이 만들어야 신뢰도 높은 퍼지 제어를 할 수 있을 것이다.