
자이로스코프, gyroscope, 회전의(回轉儀)
위아래가 완전히 대칭인 팽이를 고리를 이용하여 팽이 축에 직각인 방향으로 만들고 다시 그것을 제2의 고리를 써서 앞의 것과 직각 방향으로 지탱하여 줌으로써 팽이의 회전이 어떠한 방향으로도 일어날 수 있도록 한 장치이다. 방향의 측정 또는 유지에 사용되는 기구이다.
자이로스코프는 축이 어느 방향으로든지 놓일 수 있는 회전하는 바퀴이고 로터와 짐벌로 이루어진 하나의 메커니즘이며 각운동량 보존법칙에 근거한다. 자이로스코프가 빠르게 회전할 때에는, 외부에서 토크(torque; 회전우력-돌림힘)가 주어졌을 때 그 방향이 회전에 의한 각운동량(angular momentum)에 의해 회전하지 않을 때보다 훨씬 적게 변화하게 된다. 자이로스코프는 수평 유지 장치인 짐벌에 놓이게 되므로 외부의 토크는 최소화되며, 장착된 받침이 움직이더라도 그 방향은 거의 고정되게 된다.
자이로스코프와 비교할 만한 센서로는 가속도센서가 있다. 가속도센서는 지표면을 기준으로 기울기를 측정한다. 이 가속도센서의 특징은 물체의 움직임을 세밀하게 측정할 수 없고 외부 가속도의 합이 0이라면, 즉 등속 운동하는 물체에 대해서는 측정할 수 있는 것이 없다. 그러나 자이로스코프는 ‘각속도’를 측정하여 얻은 정보를 가지고 기울기를 측정한다. 미사일이나 항공기의 길잡이 역할을 하는 핵심 부품이기도 하고 세그웨이 PT 등에도 활용된 원리이다.
역사
역사적으로 알려져 있는 최초의 자이로스코프는 요한 보넨베르거(Johann Bohnenberger)가 1817년 만든 것인데, 그 당시 자이로스코프는 단지 '기계(machine)'라 불렀다. 프랑스의 수학자 라플라스(Pierre-Simon Laplace)는 파리의 에콜 폴리테크닉(École Polytechnique)에서 근무하면서, 이 기계를 학습교재로 사용할 것을 추천하였고, 이는 푸코(Léon Foucault)의 관심을 끌었다. 푸코는 이를 지구의 자전과 관련된 실험에 사용하였으며, '자이로스코프'라는 이름을 생각해 내었다. 지구의 회전(gyros)을 보는(scopeein) 실험은 마찰로 실패하였다. 각 실험 시간은 변화를 관측하기 어려운 8 ~ 10분으로 제한되어야 했기 때문이다.
1860년대에 들어서면서, 전기 모터가 만들어져 이 구상을 실행 가능하게 하였다.
20세기 초의 수십 년 동안, 여러 발명가들이 자이로스코프를 초기 블랙박스의 항해 장치에 이용하려 시도하다가 실패하였는데, 유사한 원리가 관성유도장치와 탄도 미사일에 쓰이게 되었다. 항해용으로 제작되어 사용할 수 있는 자이로컴퍼스는 1905년에서 1908년 사이 독일의 발명가 헤르만 안슈츠 카엠페(Hermann Anschütz-Kaempfe)가 개발하였다. 미국의 엘머 스페리(Elmer Sperry)는 1910년가 그 뒤를 따랐고, 각국에서 이 발명품의 군사적인 중요성을 인식하게 되었다. 이 시대는 해군이 국방력의 중요한 척도였고, 각자의 자이로스코프 산업을 만들어내었다. 스페리 자이로스코프사는 항공기와 군함의 안정장치를 만들었고, 다른 자이로스코프 개발자들도 이를 따랐다.
1917년, 미국 인디아나폴리스의 챈들러 회사는 당기는 줄과 축받이를 갖춘 장난감인 '챈들러 자이로스코프'를 만들었다. 이 제품은 이후 지속적으로 생산되어 미국 장난감의 고전으로 여겨지고 있다.
어떤 것은 진동하는 부품을 사용하기도 한다. 이는 'MEMS(Micro Electro-Mechanical System; 극소 전자기계장치)'라 부르는데, 이 장치를 사용한 실용적인 자이로스코프는 SDI(Systron Donner Inertial)가 제조하였다.
역할
자이로스코프
정의에서 부연으로 설명한 가속도센서와 비교하면, 가속도센서는 지표면을 중심으로 기울기, 가속도 등을 측정한다. 그러나 지표면에 대해 수직 방향의 가속도는 측정할 수 없다. 자이로스코프는 가속도센서로 측정할 수 없는 방위각을 측정한다. 다시 말해 지면에 수직인 조건에 상관 없이 모든 방면에 대해 각도의 변화를 측정할 수 있다. 가속도센서는 직선운동하지 않는 물체에 대해선 측정하는 데 어려움을 겪는다. 자이로스코프는 회전운동의 각도를 측정할 수 있기에 자이로스코프와 가속도센서의 기능을 합치면 물체의 정확한 운동을 파악할 수 있게 된다.
물체의 운동을 측정하는 데 필요한 축의 개수가 달라질 수 있다. 어떤 물체가 2차원적인 운동만 한다면 자이로스코프 1개와 가속도센서 2개가 필요하지만 어떤 물체가 3차원적인 운동을 한다면 자이로스코프 3개와 가속도센서 3개가 필요하게 된다. 가장 흔히 알려진 3차원을 측정할 수 있는 6개의 센서들을 통틀어 6자유도(Degrees of Freedom)를 가진다고 표현한다.
구조 및 기능
자이로스코프를 가장 쉽게 표현한다면 팽이라고 말할 수 있다. 회전 중인 팽이는 외력이 0인 상태에서 회전력에 대한 관성을 가진다. 팽이가 돌고 있는 지표면에 각도가 생겨도 팽이의 중심축은 지구 중심 방향을 향하는 현상을 보면 알 수 있다. 자이로스코프는 로터와 짐벌로 이루어진 하나의 메커니즘이다. 쉽게 말하자면 로터는 팽이이고 짐벌은 균형을 유지해 자유롭게 회전할 수 있는 구조이다.
방향 안정
첫 번째 특성은 방향 안정(Directional Stability)이다. 고속 회전하는 로터에 외력이 없다면 로터의 각운동량 벡터값은 항상 일정하다는 것이 방향 안정이다. 마치 뉴턴 제 1법칙인 관성의 법칙과 관련이 크다. 피겨 선수들이 빙판 위에서 회전할 때나 좀더 거시적인 범위로 보자면 지구의 자전 등이 대표적인 예이다.
균형을 잡는 것이 중요한 물체인 비행기를 예로 들면 자이로는 회전축을 중심으로 균형을 유지한다(여기서 비행기를 기준좌표계로 설정할 수 있다). 비행기가 운동하던 방향이 바뀜에도 회전자는 회전축을 중심으로 밸런스를 유지한다. 외부틀은 비행기와 함께 회전하며 비행기가 기준좌표계로부터 틀어진 정도를 측정한다.
플랫폼 방식이란 센서가 설치된 물체의 자세가 어떻게 변하든 고정된 자세를 가진 플랫폼 위에서 그 물체의 자세를 관측하는 방식이다. 공중에서 하늘과 땅을 구별하기 힘든 전투기나 글라이더 같은 비행기에 주로 사용된다.
세차운동
두 번째 특성은 세차운동(Precession)이다. 로터가 외부로부터 로터의 축 방향으로 힘을 받으면 회전 반발력(Gyroscopic Reaction Moment)이 생겨 로터에 수직한 또 다른 수직축 방향에 대한 회전운동을 시작한다. 오토바이를 예로 들면 오토바이가 빠른 속력을 낼 때, 핸들을 직접 조종하지 않고 몸을 한쪽으로만 기울여도 자신이 주행하던 방향을 바꿀 수 있다. 오토바이를 기준으로 왼쪽으로 몸을 기운다면 오토바이 바퀴의 윗부분에 대해 왼쪽 지면으로 미는 힘이 발생한다. 바퀴의 윗부분에서 왼쪽 지면으로 미는 힘은 90도가 지난 바퀴의 앞부분에서 작용하여 왼쪽으로 밀리는 결과가 나타나 오토바이가 왼쪽으로 방향을 바꾸게 된다.
회전하는 팽이의 회전운동은 회전축을 중심으로 이루어진다. 만약 이 팽이에 외력을 가하거나 시간이 지나 팽이가 스스로 멈추려 할 때, 축을 중심으로 회전하고 있으나 회전축 또한 일정한 원 모양의 자취를 그리면서 회전하는 것을 관찰할 수 있다.
회전운동을 방해하는 외력이 크다면 팽이는 멈출 것이고 작다면 팽이는 다시 중심을 잡고 회전할 것이다. 이런 현상을 세차운동이라 정의한다.
이러한 세차 운동은 각운동량 보존법칙에 의한 내용이며 각운동량 보존에 의하면 각운동량의 방향만 바뀔 수 있고 이 방향의 변화는 토크와 같기 때문에 세차운동을 하게 되는 것이다.
자이로센서
자이로스코프가 내재된 물체가 회전운동을 하면 생기는 회전 반발력을 측정하여 전기신호로 바꾸는 장치를 추가한다면 그것은 자이로센서로 활용될 수 있다. 관성항법장치(INS)는 가속도센서와 자이로센서의 기능을 활용한 장치로 자세나 위치를 추정할 수 있다. 관성 좌표계에서의 운동을 측정하여 이동거리와 방향을 계산해내는 것으로 오늘날 스마트폰에서 애용되고 있다. 3차원 공간에서 물체의 동선을 완벽하게 파악할 수 있는 기술이 발명되었다고 해도 과언이 아니다.
광학식 자이로센서
광학식 자이로센서는 사냑효과(Sagnac Effect)를 이용한 자이로센서로 링레이저(RLG) 자이로센서와 광섬유(FOG) 자이로센서로 구분된다.
광로를 따라 동시에 빛(레이저)을 방사하면 양방향에서 접근하는 빛이 같은 시간에 검출된다. 하지만 △t만큼 회전운동이 발생하면 두 빛의 도달시간은 달라지게 된다. 그 차이를 검출·계산하여 각속도 Ω를 산출한다. 링레이저 자이로센서는 이 효과에 의한 공진기 길이의 변화를 이용하고, 광섬유 자이로센서는 길게 감긴 광섬유를 이용하여 광로의 길이변화를 측정하여 각속도를 산출한다. 광학식 자이로센서는 구조가 간단하지만 스마트폰에 사용하기에는 가격과 크기가 적합하지 않다.
MEMS 자이로센서
스마트폰 안에 탑재된 자이로센서는 코리올리 힘을 측정하는 소리굽쇠 방식의 MEMS 센서로 소형 모바일 기기에 채용된 자이로센서는 대부분 MEMS 방식이다. 소리굽쇠 방식이란 무한 진동하는 추 2개를 이용하여 회전을 측정할 수 있도록 하는 방식이다. 항상 일정한 자세를 유지하는 짐벌식과는 달리 MEMS 방식의 센서들은 대상체에 안정된 플랫폼을 고정(strap)한 상태에서 자세를 측정하는데, 플랫폼에 장착된 대상체가 원래의 위치에서 달라지는 만큼을 전기신호로 주고 이를 받아서 자세 변화를 감지한다. 이런 방식을 스트랩다운(strapdown) 방식이라고 부르기도 한다.
응용
스마트폰
스마트폰에 상하좌우 동작을 감지하는 자이로스코프 센서를 내장하여 다양한 동작을 인식하는 게임 등 애플리케이션 개발이 가능하다. 자이로스코프는 3개 축으로 동작을 인식하여 균형감과 입체감을 정밀하게 감지할 수 있다.
드론
드론 ‘짐벌’(Gimbal)은 재해 지역 탐구 등 고급 용도에 활용이 가능한 기기로, 축구공처럼 오각형과 육각형으로 구성된 외피가 입혀져 있고 중앙에는 비행에 필요한 로터, 제어시스템, 안정판 등이 장착된 본체가 들어있다. 짐벌의 특징은 본체를 탑재하는 방법인데, 자이로스코프 및 나침반과 같은 장치가 탑재되어 있고 바깥 부분의 움직임이 내부에 전해지기 어려운 구조로 설계되었다. 기존의 드론은 본체가 장애물에 닿을 경우 로터가 영향을 받아 기울어졌지만, 짐볼은 바깥 쪽 부분이 회전해 충격을 받아 넘기기 때문에 균형을 유지한다.
자이로스코프 배경이론
1. 기본 개념 - 토크와 각운동량
• 토크의 정의: τ=r×F
• 각운동량의 정의 : L=r×p
• 각운동량과 토크사이의 관계식 : τ=dL/dt
• τ =0일 때 각운동량은 상수
• →각 운동량 보존 법칙(Angular Momentum Conservation)

2. 기본 개념 – 관성 모멘트
• 관성모멘트 – 회전 상태를 유지하려는 정도
• 자이로스코프 바퀴의 관성모멘트 측정
• 뉴턴의 2법칙 : F=ma=mg-T
• 장력 T =mg-ma=mg-a
• 바퀴를 회전시키는 토크
• τ=rT=rm(g-a)
• a=rα (α: 각가속도)
• 바퀴의 관성모멘트 I : I=τα=rm(g-a)a/r=mr2ga-1
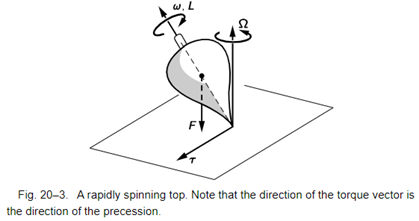
3. 팽이의 질량중심에 작용하는 중력이 만드는 토크
• 토크의 영향으로 수직축을 중심으로 세차운동
• 원뿔모양 궤적을 그린다.
• τ=dLdt=Ω×L0
• 고속으로 회전하는 팽이에 토크가 작용해서 나타나는 토크는 토크 방향으로 발생
• 토크 방향과 토크를 일으키는 힘은 서로 직교
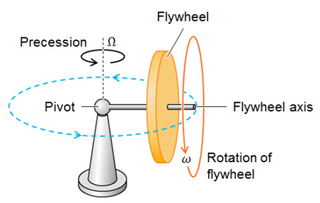
4. 만일 바퀴가 회전하지 않는다면?
• 축의 한 끝이 지지된 자이로스코프
• 관성 바퀴가 회전하지 않는 경우:
• 자유단 쪽이 중력에 의한 토크를 받아 낙하
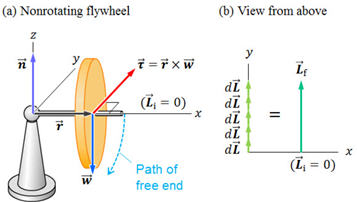
• 초기 각운동량 0
• 시간 dt경과할 때마다 토크에 의해 각운동량 변화
• 각운동량과 토크 방향이 동일
• 바퀴 아래로 떨어짐
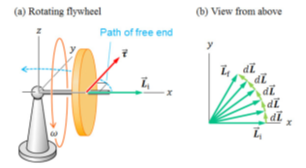
5. 만일 바퀴가 회전한다면?
• 바퀴가 회전하면 초기 각운동량 Li 존재
• 관성바퀴에 작용하는 토크가 회전축에 수직
• 각운동량의 변량dL도 L_i와 수직
• 원운동과 비슷함
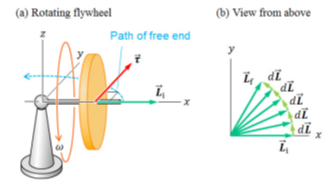
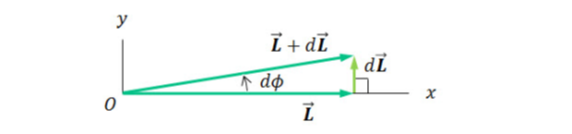
6. 세차 각속도
• 시간 dt동안 자이로스코프 회전축이 움직인 각도는 dϕ=|dL||L|
• 자이로스코프의 세차 각속도 Ω=dϕdt =|dL/|L|dt=τzLz=wrIω
• 관성 바퀴의 회전 각속도 ω 와 반비례관계
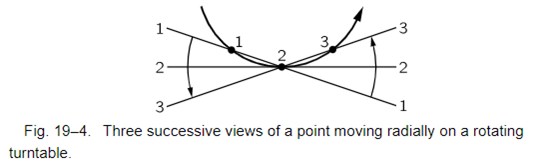
7. 심화 - 힘과 가속도만으로 토크를 이해하자.
• 바퀴가 원운동을 할 때 입자들은 한 평면 위에서 얌전히 운동하는 것이 아님
• (Fig 19.4)휘어진 경로 따라서 운동 -> 측면으로 힘이 작용하는 중
• 무슨 힘?
• 회전축을 들어올리는 사람의 힘!
• 바퀴의 반대쪽에서 회전하는 입자는 반대 방향으로 힘 작용
• 알짜힘은 0
• 바퀴가 강체이므로 축의 힘이 바퀴까지 전달됨
• 바퀴를 들어올리기만 하면 됨
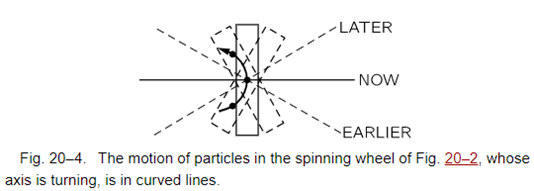
8. 장동 운동(Nutation)
• 지금까지 관성 바퀴의 회전에 의한 영향만 고려
• 각운동량 L이 평면상에서 움직인다고 가정
• 그러나 실제로는 세차운동에 의한 각운동량의 수직 성분 존재
• 따라서 짧은 주기로 수직으로 진동하는 장동 발생
• 회전하는 팽이의 축을 가볍게 잡아 수직으로 세우면 중력에 의한 토크는 0
• 손을 놓으면 중력에 의한 토크 발생 → 팽이는 기울어진다.
• 기운 채로 옆으로 돌아간다.
• 이 회전이 계속되기 위해서는 어떤 토크가 계속 필요
• 이 토크가 없으면 자이로스코프는 쓰러지기 시작한다. → 수직축 토크 발생
• 실제 운동은 균일한 세차 운동을 위한 속도와 다름
• 회전축은 원래 출발한 높이로 다시 상승
• 사이클로이드 궤적 완성

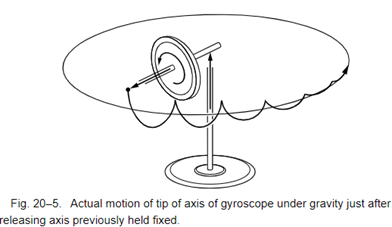
장동 운동에서 자전축이 내려가는 이유?

• 장동은 마찰 때문에 매우 빠르게 감쇠하는 사이클로이드 궤적을 그림
• 균일한 세차 운동으로 바뀜
• 운동이 안정되면 자전축이 원래 출발 위치보다 내려감 → 왜?
• 자전축이 수평을 향하도록 조절하면 그 위치를 유지하며 돌아갈까?
• 세차운동 식에 의하면 될 것 같은데?
• 바퀴는 세차운동에 대해 약간의 관성모멘트를 가짐
• 축에 대한 각운동량도 존재
• 각운동량은 누가 제공???
• Pivot 은 고정돼 있으니 수직축 토크는 0
• 토크 0인데 각운동량 변화가 있다고??

진동 중심 |
• 사이클로이드 궤적을 그리며 장동하는 축은 진동의 가운데 축으로 수렴
• 가운데 지점은 처음 출발 위치보다 아래쪽
• 자전축이 더 기울었으니 각운동량은 약간의 수직성분 가짐
• 이 값은 세차운동이 계속되기 위한 양과 일치
• ∴ 세차운동이 계속되기 위해서는 조금 숙여야 함
• 안정된 운동을 위해 중력에게 조금 양보한 것