인수분해

대수학
Algebra
인수분해, factorization, 因數分解
어떤 원소를 다른 원소의 곱으로 표현하는 것이다.
대부분 중3 단원에서 곱셈 공식 & 이차방정식과 함께 나온다고 하지만, 사실 초등학교 5학년 시절 나온 통분과 약분부터 이름만 안 알려졌을 뿐 이 때부터 존재가 알려지다가 중학교 1학년 때 분배법칙이 나오면서 일차식의 인수분해를 알게 되다가 중학교 3학년 때 그 이름이 공개된다.
정수 위에서의 인수분해
소인수분해를 하는 방법
이 문단에서는 1보다 큰 어떤 정수
N
N이 주어졌을 때, 10진법 표기에서 약수를 찾는 여러 가지 기술에 대해 소개한다. 먼저 사람의 입장에서 가장 쉬운 방법은 아래의 배수 판정법을 이용하는 것이다.
정수
N
N에 대해서,
2의 배수: 일의 자리 숫자가 짝수.
3의 배수: 각 자릿수의 합이 3의 배수.
4의 배수: 맨 뒤 두 자리가 00이거나 십의 자리가 짝수인 10의 배수나 십의 자리가 홀수면 1의 자리가 2/6, 아니면 0/4/8, 0 이하면 그냥 4의 배수
5의 배수: 일의 자리가 0이거나 5인 경우.
6의 배수:
N
N이 2의 배수이면서 3의 배수.
8의 배수: 맨 뒤 세 자리가 000 또는 8의 배수.
9의 배수: 각 자릿수의 합이 9의 배수.
10의 배수: 일의 자리가 무조건 0.
10n의 배수: 가장 끝의 n개의 자리가 모두 0.
7, 11, 13의 배수: 일의 자리부터 세 자리씩 끊은 뒤, 각 부분을 교대로 빼고 더한 값이 7, 11, 13의 배수.
15의 배수:
N
N이 5의 배수이면서 3의 배수.
25의 배수: 맨 뒤 두 자리가 00 또는 25의 배수(25, 50, 75)
12의 배수:
N
N이 3의 배수이면서 4의 배수.
20의 배수:
N
N이 4의 배수이면서 5의 배수.
30의 배수:
N
N이 5의 배수이면서 6의 배수.
48의 배수:
N
N이 3의 배수이면서 16의 배수.
72의 배수:
N
N이 8의 배수이면서 9의 배수.
27, 37의 배수: 일의 자리부터 3자리씩 끊은 뒤 이들을 모두 합한 결과가 27, 37의 배수인 수.
보다 일반적으로 n이 합성수이고, 소인수가 2개 이상일 때, n의 배수를 판별하는 방법은 d가 n의 유니타리 약수라고 했을 때 d와 n÷d의 공배수 여야 하므로 이 둘의 배수판정법을 동시에 만족해야 한다는 것이다.
또는 아래 정리를 사용할 수도 있다.
모든 합성수는 그 수의 제곱근보다 작거나 같은 약수를 갖는다.
인수분해, 인수분해 공식(고1)
인수분해는 전개의 반대과정
전개할 때는 공셈공식을 사용하니까 인수분해는 공셈공식을 거꾸로 사용
따라서 인수분해 공식이라고 따로 외우는 게 아니라 곱셈공식의 좌, 우변을 바꾸면
인수분해공식
인수분해는 하나의 다항식을 두 개 이상의 다항식의 곱으로
그 곱을 이루고 있는 다항식을 인수라고 하고요. 숫자의 약수와 비슷

인수분해를 할 때 가장 먼저 해야 할 일은 공통인수로 묶는 거
공통인수로 묶은 다음에 공식을 적용
공통인수가 없다면 바로 공식을 사용
인수분해는 전개의 반대과정이니까 곱셈공식의 좌, 우변을 바꾸기만 하면 인수분해 공식
먼저 중학교 때 공부했던 인수분해 공식 다섯 개를 확인
a2 ± 2ab + b2 = (a ± b)2
a2 - b2 = (a + b)(a - b)
x2 + (a + b)x + ab = (x + a)(x + b)
acx2 + (ad + bc)x + bd = (ax + b)(cx + d)
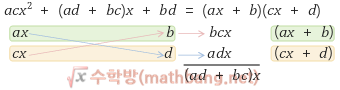
다음은 곱셈공식, 곱셈공식 유도에서 했던 공식들의 좌, 우변을 바꾼 인수분해 공식
(1) ma + mb + mc = m(a + b + c)
(2) a2 + b2 + c2 + 2(ab + bc + ca) = (a + b + c)2
(3) a3 + 3a2b + 3ab2 + b3 = (a + b)3
a3 - 3a2b + 3ab2 - b3 = (a - b)3
(4) a3 + b3 = (a + b)(a2 - ab + b2)
a3 - b3 = (a - b)(a2 + ab + b2)
(5) a3 + b3 + c3 - 3abc = (a + b + c)(a2 + b2 + c2 - ab - bc - ca)
=
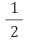
(a + b + c){(a - b)2 + (b - c)2 + (c - a)2}
(1)번은 인수분해의 가장 기본인 공통인수로 묶기
(2), (3), (4)는 곱셈공식을 거꾸로
(5)의 아랫줄에 있는 공식은 곱셈공식의 변형에서 했던 a2 + b2 + c2 - ab - bc - ca =
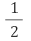
{(a - b)2 + (b - c)2 + (c - a)2}을 적용
다음을 인수분해하여라.
(1) x2 - 5x + 6
(2) x3y - xy3
(3) 4x2 + y2 + 9z2 + 4xy - 6yz - 12zx
(4) x3 - 3x2y + 3xy2 - y3
인수분해는 공통인수로 묶은 다음에 인수분해 공식을 이용
(1)은 공통인수가 없네요. X자를 이용해서 해도 좋고, 공식을 이용
x2 - 5x + 6 = (x -2)(x -3)
(2)은 두 항에 xy라는 공통인수가 있어요. 이걸로 묶고 공식을 적용
x3y - xy3 = xy(x2 - y2) = xy(x + y)(x - y)
항을 잘 보면 제곱인 항이 3개가 있으니까 위 인수분해 공식에서 (2)번에 해당하는 문제
a2 + b2 + c2 + 2ab + 2bc + 2ca = (a + b + c)2
4x2 + y2 + 9z2 + 4xy - 6yz - 12zx
= (2x)2 + y2 + (-3z)2 + 2(2x)y + 2y(-3z) + 2(-3z)(2x)
= (2x + y - 3z)2
(4)번은 세제곱인 항이 두 개있고, 이들이 섞여 있는 항이 두 개니까 (3)번 공식에 해당하는 문제
그런데 y3이 (-)
a3 ± 3a2b + 3ab2 ± b3 = (a ± b)3
x3 - 3x2y + 3xy2 - y3
= (x - y)3
위처럼 여러 가지 인수분해 공식들이 있다. 간단한 것은 단순히 다항식의 전개식의 양 변을 바꾸어 놓은 것처럼 보이지만, 어디서 갑툭튀했는지 모르는 것들도 가끔 있다. 따라서 하나씩 곱해가면 되는 전개와는 달리, 인수분해는 그때 그때 공식 및 유형을 외워서 문제풀이에 써먹는 것이 정신 건강에 이롭다. 하지만 암기만으로는 한계가 있으니 여러가지 방법을 익혀놓는 것도 중요하다. 인수분해 공식을 증명하기 위해서는 인수분해된 식을 다시 전개해 보면 된다. 고등학교 수학을 배운 사람이라면 다 알듯 인수분해는 고등학교 수학 및 대수학 그 자체에 있어서 없어서는 안 될 존재로, 이것을 배우지 않고 수학을 배운다는 것은 있을 수 없는 일이다.
이름이 비슷한 것으로, 합성수를 소수의 곱으로 고치는 소인수분해가 있다. 인수분해와 방법은 다르지만, 수학적인 의미는 같다고 볼 수 있다. 실제로 인수분해의 대수학적 의의는 소인수분해가 합성수를 소수의 곱으로 고치는 것처럼 다항식을 기약다항식의 곱으로 고치는 것이다. 배수와 약수, 인수분해의 성질이 수나 다항식에서나 똑같이 성립한다는 것은 꽤나 중요한 사실이고, 중등교육에서 암묵적으로 사용되지만 정확히 언급되지는 않는 내용. 실제로 산술의 기본정리와 대수학의 기본정리의 따름정리는 꽤나 닮아있다.
인수분해에 염증을 느끼지만 수학에 흥미를 느끼고 싶은 학생들에게 팁을 몇 가지 주자면, (대수학의 기본정리에 의해) 모든 다항식은 복소수 범위 내에서 인수분해를 할 수 있는데, 그래서 진짜로 복소수 범위에서 인수분해를 하면 상당히 흥미로운 결과가 나온다. 당장 저 인수분해 8번 공식이 삼차방정식의 근의 공식 유도에 중요한 역할을 하게 된다.
고등학교 1학년에서 미지수가 3개인 이차식, 3차, 4차식의 인수분해 공식이 나온다.
누군가, 또는 무언가를 제거하는 것을 인수분해라고 표현하기도 한다. 디시인사이드에서 아햏햏이 유행하던 시절부터 홍성대와 엮여서 나왔던 오래된 말장난이다. 예시를 몇 개 들자면 팀 포트리스 2의 스카웃의 커스텀 서버 언락 무기 중 'Atomizer'의 번역명이 '인수분해'이고, 신세계에서도 나왔다.
고등학교 입학하면 인수분해를 또 배울 건데, 중학교 때 배운 삼각형의 성질과 피타고라스의 정리를 엮어서도 많이 나온다.
곱셈 공식과 더불어 수포자가 본격적으로 속출하는 구간으로도 알려졌다.