의사결정 나무(Decision Tree) 기법
⦁ 의사결정이 단계별로 연속적으로 이루어지는 경우에 사용할 수 있는 분석 기법으로 1964 년에 매기(J.F Magee)에 의해서 제기도었으며, 생산규모 확장 시기 결정에 이용되는 확률적 기법으로 의사결정에서 고려되는 대체안의 구조를 여러 갈래의 가지와 마디를 갖고 있는 나무 모양으로 나타낸 것
- 의사결정 문제가 단일 기간에 국한되지 않고 여러 기간에 걸쳐 연속적으로 영향을 주게 될 때 최초의 의사결정이 전 기간에 걸쳐 미치는 영향을 고려하여야 하므로 각 기간별로 의사결정이 이루어져야 할 경우에 사용함.
⦁ 수요가 불확실하고 순차적으로 여러 의사결정을 내려야 하는 다양한 경우를 평가하는데 유용
- 제품계획, 프로세스 설계, 프로세스 용량, 입지 등의 운영 관리와 공급 사슬 관련 의사결정에서 폭넓게 사용됨.
⦁ 가능한 대안들을 그것들의 결과와 함께 표현한 도식적 모형
∎ 작성 방법
⦁ 사각형 결정 마디( □ ) : 어떤 결정을 하는 상태를 나타내는 의사결정을 내리는 지점
⦁ 원형 사건 마디( ○ ) : 의사결정자의 선택과 상황과의 결과를 설명하는 상황 발생점
⦁ 가지 : 의사결정 또는 상황 발생점에서 뻗어 나온 가지는 의사결정의 대안을 표시하기도 하고 선택과 상황이 이루어질 때 다양한 결과를 의미하기도 함.
① 사건 마디에 대해 각 사건 가지의 보상과 확률을 곱하고 이들을 모두 더하여 사건 마디의 기대 보상을 계산함.
- 상황 발생점에서는 상황 발생점에서 뻗은 가지에 있는 미래상황의 발생 확률과 성과를 곱한 결과의 합을 기입하고 이를 위치 값이라 하며 상황 발생점 왼쪽에서 뻗어 나온 가지의 성과가 됨.
② 결정 마디에선 기대 보상이 가장 높은 대안을 선택
- 의사결정시 각 대안의 위치 값을 비교하여 최선의 대안을 선택하여 기입
(예제 1)
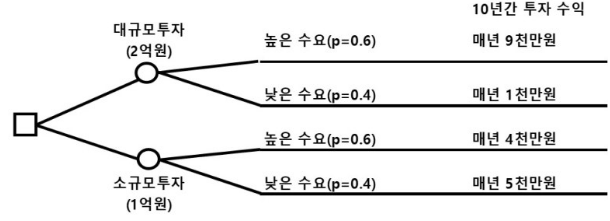
신제품은 앞으로 10 년간 계속 판매하며 수요가 높을 확률은 60%, 낮을 확률은 40%이며, 시설투자는 대규모 투자시 2억 원이고 소규모로 할 경우 1억 원임.
수익은 대규모 시설에서 수요가 높으면 10 년간 매년 9천만 원, 수요가 낮으면 1천만 원이고 소규모 시설에서 수요가 높으면 4천만 원, 수요가 낮으면 5천만 원일 때 디시전 트리(Decision Tree)를 작성하고 기대수익을 계산한 후 유리한 전략을 선정
∎ 의사결정 나무 - AON 네트워크 적용
∎ 기대수익의 계산
|
선택
|
외부 조건
|
투자액
|
확률
|
연간 수익
|
수익(10 년간)
|
기대수익
|
|
대규모 투자
|
높은 수요
|
(-) 2억
|
0.6
|
0.9억
|
5.4억
|
3.8억
|
|
낮은 수요
|
0.4
|
0.1억
|
0.4억
|
|||
|
소규모 투자
|
높은 수요
|
(-) 1억
|
0.6
|
0.4억
|
2.4억
|
3.4억
|
|
낮은 수요
|
0.4
|
0.5억
|
2.0억
|
※ 기대수익은
대규모 투자 = 10년 간 수익 – 투자액 = (5.4 + 0.4) – 2 = 3.8억 원
소규모 투자 = (2.4 + 2.0) - 1 = 3.4억 원
∎ 결론 : 기대수익의 계산에서 대규모 투자의 기대수익이 소규모 기대수익 보다 크므로 대규모 투자를 선택함.
(예제 2)
새 입지에 대형 시설과 소형 시설 가운데 하나를 지으려고 하며 이 지역의 수요는 작을 확률이 0.4, 클 확률이 0.6으로 추정함.
소형 시설을 건설했다가 수요가 크면 확장할 수도 있고(보상=270,000달러), 하지 않을 수도 있음.(보상=223,000달러)
소형 시설을 건설했다가 수요가 작으면 확장할 이유가 없으며 이때의 보상은 200,000달러
대형시설을 건설하였다가 수요가 작으면 아무 일도 하지 않든가(보상=40,000달러), 지역광고를 통해 수요를 자극할 수 있으며 광고에 대한 반응은 미미할 수도 있고(확률 0.3, 보상=20,000달러) 클 수도 있음.(확률 0.7, 보상=220,000달러)
대형시설을 지었는데 수요가 큰 경우엔 보상이 800,000달러임.
어떤 규모의 시설을 지어야 하는가?
(풀이)
∎ 의사결정 나무 - AOA 네트워크 적용

1) 대형시설의 경우
광고 시 전개되는 효과 : 0.3 x 20 + 0.7 x 220 = 160
광고를 하는 것(160)이 안 하는 것(40)보다 좋기 때문에 결정 마디 3의 기대 보상은 160
대형시설의 기대 보상은 0.4 x 160 + 0.6 x 800 = 544임.
2) 소형 시설의 경우
확장하는 것이 안 하는 것보다 낫기 때문에 결정 마디 2의 기대 보상은 270
소형 시설의 기대 보상은 0.4 x 200 + 27 x 0.6 = 242임.
3) 결론 : 따라서 기대 보상이 가장 큰 대형시설 대안을 선택함.
(예제 3)
스키장 리프트 한 대는 하루 250명을 수용할 수 있으며 스키 시즌은 보통 12월에서 4월까지 14주 동안으로 이 기간 동안 리프트는 매주 7일씩 가동됨.
리프트 이용률은 경기에 영향을 받으며 경기가 불황(0.3), 보통(0.5), 호황(0.2) 일 확률임.
경기가 불황이면 첫 번째 리프트만 이용률이 90%이며,
경기가 보통이면 첫 번째 리프트 이용률은 100%이고 두 번째 리프트 이용률은 50%임.
경기가 호황이면 첫 번째 리프트 이용률은 100%이고 두 번째 리프트 이용률은 90%임.
새로운 리프트를 신설할 경우 화폐의 시간 가치와 경제적 수명을 감안한 구매 비용은 1대 당 5만 달러이나 리프트 두 대를 동시에 구매한다면 연간비용은 9만 달러임.
가동 시 이용률과 무관하게 대당 리프트 운영비용은 20만 달러이며, 리프트 탑승권은 고객 1인 당 하루에 20달러일 때 이 스키장에선 리프트를 몇 대 설치해야 하는가?
(풀이)
* 연간 수입량 : 250 x 7 x 14 x 20 = 490,000 달러
* 1대인 경우 고정비 : 5만 + 20만 = 250,000 달러
2대인 경우 고정비 : 9만 + 20만 x 2대 = 490,000 달러
∎ 의사결정 나무- - AOA 네트워크 적용

2) 기대 수익표
|
대안
|
경제 사정
|
보상(수입-비용), 천 달러
|
결과
|
|
|
수입
|
비용
|
|||
|
1 대
|
불황(0.3)
|
0.9 x 490
|
리프트 신설 비용 50,
대당 운영비용 200
|
191
|
|
보통(0.5)
|
1 x 490
|
240
|
||
|
호황(0.2)
|
1 x 490
|
240
|
||
|
2 대
|
불황(0.3)
|
0.9 x 490
|
90 + 1 x 200
|
151
|
|
보통(0.5)
|
(1 + 0.5) x 490
|
90 + 2 x 200
|
245
|
|
|
호황(0.2)
|
(1 + 0.9) x 490
|
90 + 2 x 200
|
441
|
|
여기서 주의할 점은 2대를 투자하였는데, 불황인 경우 이용율이 90%로 두대를 투자하였지만 한대만 운용하므로 1대의 운영비용만 반영하여야 함.
1) 1대 설치 시 기대 보상 : 0.3 x 191 + 0.5 x 240 + 0.2 x 240 = 225.3 천 달러
2) 2대 설치 시 기대 보상 : 0.3 x 151 + 0.5 x 245 + 0.2 x 441 = 256 천 달러
결론 : 리프트 2대를 설치함.
잡스9급 PDF 교재

✽ 책 구매 없이 PDF 제공 가능
✽ adipoman@gmail.com 문의
✽ 유튜브 강의