벡터, vector, 영 벡터(Zero Vector), 단위 벡터(Unit Vector), 위치 벡터(Position Vector), 거리 벡터(Distance Vector), 법선 벡터(Normal Vector), 방향 벡터(Direction Vector), 동경 벡터(Radius Vector)
1. 벡터 (Vector)
ㅇ 이공학 분야에서 많이 사용되는 수학적인 양(量) 표현 기법
- 거리, 무게, 속력 등 크기만을 나타내는 1차원적인 양(量)인 스칼라와는 달리,
- 힘,속도 등과 같이 크기(量) 및 방향(方向) 등 2차원 이상의,
- 즉, 2 이상의 원소(요소)들에 의해, 어떤 양(量)을 표현하는데 유용한 표기법
2. 벡터의 여러 정의들
ㅇ 기하학적인 측면 : 유향 선분
- 크기 및 방향에 의한 표현
. 例) 힘, 모멘트, 변위, 속도, 가속도, 운동량, 열유동 등
ㅇ 대수적인 측면 : 수 또는 함수들의 나열
- 실수 또는 복소수 또는 함수를 원소(성분)로 갖는 순서쌍(Ordered Pair/n-tuple)
. 例) 좌표, 벡터 함수 등
ㅇ 추상적 대상(object) : 벡터공간 상에서 대수적 성질을 갖는 것
- 대수적 성질을 공리로 이용한 벡터공간 내의 대상을 추상화한 것
. 例) 무한 실수 수열, 연속 함수, 행렬 등도 벡터 형태로 나타낼 수 있음
3. 벡터의 표기
ㅇ 기하학적 측면 : 시작점과 끝점(통상,작용점)을 연결하는 유향선분으로 표시
- 벡터는 획이 굵은 활자체 문자 또는 문자 위에 윗 화살표를 그어 표기

ㅇ 대수적 측면 : 소문자 볼드체로 표시

4. 벡터의 특징
ㅇ 수학적 도구
- 벡터는 대수학적인 면과 기하학적인 면 모두를 가진 수학적 도구.
ㅇ 일반화된 표현
- 벡터는, 좌표계와 무관하게 (독립적으로), 기하학적 정리, 물리법칙, 이론들을 표현할 수 있음.
ㅇ 간결성
- 벡터는 벡터 미분연산자 등을 이용하여 간결하고 일반적인 방법으로 표시하기가 용이함.
5. 기하학에서의 벡터 (벡터에 대한 기하학적인 접근방법)
ㅇ 벡터의 기하학적 표현
- 화살꼴(arrow) 또는 방향선분(directed line segment) 표현
. 벡터를 기하학적 길이(크기)와 방향을 갖는 양(量)으로 표현
.. 시작점 및 끝점에 의한 유향선분(有向線分)으로 크기 및 방향을 표현
- 벡터를 그 크기 및 두 벡터 간의 각도에 의해서도 표현하기도 함 (극좌표 표현)
- 例) 위치 벡터, 거리 벡터, 장(場) 벡터 등
ㅇ 벡터의 차원(Dimension)
- 기하학적 벡터 개념은 물리학/공학에서 대부분 2차원(R2), 3차원(R3)에서 이루어지나,
- 보다 고차원 공간(Rⁿ)에서의 벡터로 확장될 수 있음
6. 대수학에서의 벡터 (벡터에 대한 대수학적인 접근방법)
ㅇ 벡터의 성분 (component)
- 벡터를 좌표 성분들인 수(좌표값)의 대수적 집합으로 표현할 수 있음
ㅇ 벡터의 차원 (Dimension)
- n-차원 벡터
. n개의 원소를 갖는 벡터 = n개 원소를 갖는 순서쌍(n-tuple) :
ㅇ 벡터를 보다 추상적인 개념으로 확장이 가능
- 대수학에서 말하는 벡터는, 기하학적 벡터 개념에서의 확장 임
. `벡터 공간`이라는 정의 내에서의 대상(object)를 말함
.. 이 경우에 함수(Function)도 벡터로 볼 수 있음
- [참고] ☞ 벡터공간(Vector Space), 행렬(Matrix), 대수구조, 유한체 등...
7. 벡터의 연산
ㅇ 벡터의 상등(동등) ☞ 벡터 상등 참조
ㅇ 벡터의 크기 (|x| 또는 ‖x‖) ☞ 노름 참조
ㅇ 벡터의 정규화 (n = x/|x|) ☞ 벡터 정규화, 단위 벡터 참조
ㅇ 벡터의 대수적 연산 (선형 연산) ☞ 벡터 연산 참조
- 벡터의 덧셈
- 벡터의 곱셈 (스칼라곱셈,내적,외적,직접곱)
ㅇ 벡터의 미분,적분
- 벡터 함수 : 임의의 점에서 벡터로 주어지는 함수 F(t) = ( f₁(t), f₂(t), f₃(t) )
- 벡터 미분 연산자 : 델 연산자 ∇
. 기울기 연산자, 발산 연산자, 회전 연산자 등 참조
벡터 종류
1. 영 벡터(Zero Vector)
ㅇ 방향이 없고 길이/크기/노름이 0인 벡터 (zero vector)
- 모든 성분이 0인 벡터 : 0 = (0,0,...,0)
. Rn 공간 상에서 원점이라고도 불림
* 영 벡터는, 방향을 갖지 않는 유일한 벡터임
2. 단위 벡터(Unit Vector)
ㅇ 크기(노름)가 1인 벡터
- u = x/||x||
- ||u|| = 1
3. 위치 벡터(Position Vector)
ㅇ 원점에서 임의의 점까지 향하는 벡터

4. 변위 벡터(Displacement Vector)
ㅇ 중간경로에 관계없이 시작점과 끝점을 가장 짧게 연결하는 벡터

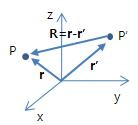
5. 거리 벡터(Distance Vector)
ㅇ 두 점간의 거리를 나타내는 벡터 표기 : R = r-r'
6. 법선 벡터(Normal Vector)
ㅇ 직선 또는 평면벡터 x에 수직(직교)하는 벡터 n
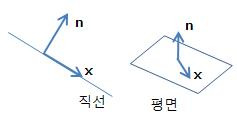
ㅇ (법선의 벡터 방정식) n x = 0
ㅇ 例)
- 직선의 길이 요소 (ndl) : 선 법선 벡터
- 표면의 넓이 요소 (da 또는 nda) : 면 법선 벡터(Surface Normal Vector)
. 관례적으로, 유향 법선 벡터의 방향은, 윗 방향 +, 아래 방향 - 로 함
- 단, 부피 요소(dv = dxdydz)는, 방향 없는 스칼라량 만 가능
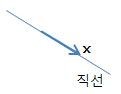
7. 방향 벡터(Direction Vector)
ㅇ 주어진 직선 방향과 평행하는 벡터
- x = tx (직선의 벡터 방정식)
8. 동경 벡터(Radius Vector)
ㅇ 고정된 시초선(또는 기선)을 기초로 하여 회전하는 반 직선 형태의 벡터
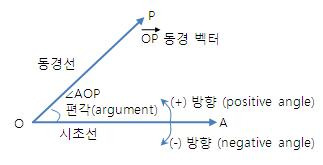
ㅇ 또는, 기준점(원점)에서 대상 점까지 그은 직선을 벡터로 한 것
벡터(Vector)
전자기학의 가장 처음에 나오는 것이 벡터이다. 뭐 물리량을 표현하는 방법 중 스칼라와 벡터가 있다고 하는데 아무튼 벡터는 크기 그리고 방향으로 결정된다는 개념은 대부분이 알고 있을 것이라고 생각한다.

벡터가 필요한 이유
벡터양(vector quantity)는 공간 내에서 크기와 방향 둘 다 갖는다고 이야기했다. 우리는 온도가 높고 낮음을 스칼라의 양으로 표현한다. 영하-18도 영상 30도 등 이런 값을 스칼라라고 하는 것은 쉽다. 하지만 그림처럼 구의 온도는 몇 도인가? 대충 빨간 곳이 뜨겁고 파란 곳이 차가운 곳이라고 이야기할 수 있지만 어떠한 표현을 딱 집어서 측정하지 않는 이상 이 구의 온도가 몇 도인지 이야기할 수 없다. 이러한 예시와 같이 지구의 중력계와 자계, 케이블 내의 전위 경도 등 이러한 것들이 벡터 계의 예이다. 어느 한 지점의 값을 알기 위해서 우리는 방향이 필요한 것이고 그래서 어떠한 곳의 위치 그리고 시간에 따라 달라지기 때문에 우리는 벡터라는 새로운 개념이 필요하다.
단위벡터
이제 왜 벡터가 필요한지 알게 되었다면 우리는 수학의 사칙연산을 기본으로 배우듯이 벡터의 사칙연산에 대하여 알아야 한다. 위의 그림에서 A에 관한 벡터 값을 알기 위해서는 3가지 즉 X, Y, Z 축으로 나누어 생각해 볼 수 있다. 3차원이기 때문에 3가지의 성분을 이용하여 벡터의 값을 말할 수 있는 직각 좌표계를 사용하여 설명하는 방식이다. 덧셈과 뺄셈은 교과서를 보면서 이해하면 되지만 곱셈에서 벡터는 약간 문제가 생긴다. 2차원 공간에서 7*6 = 42처럼 이렇게 쉽게 구할 수 없고 방향을 고려해야 하기 때문에 이러한 연산은 시각화하기가 쉽지 않다.
벡터는 어디서 시작했는가가 중요한 것이 아니라 어느 방향으로 얼마큼 움직였는지가 중요하다. 단위벡터란 크기는 다르지만 방향은 같은 기준이 되는 벡터 나는 항상 왜 크기가 1인 값을 가지는 벡터를 단위벡터라고 하는지 그리고 그것이 왜 필요한 것인지를 고민해 왔다. 이 사진 위에 있는 오른쪽 그림을 보자 크기가 1인 단위 벡터를 표현해 보았다. 방향은 같아야 하고 크기가 1이라고 가정하면 위의 영점에서 시작하는 작은 벡터는 단위벡터라고 할 수 있다. 단위벡터를 사용하는 가장 큰 이유는 곱셈을 쉽게 하기 위해서이다. 단위벡터를 구하는 과정은 nomalizing(정규화)라고 하고 즉 기준을 잡는 것이다.
(크기가 1이라는건 x축으로 1, y축으로 1, z 축으로 1칸이라는 뜻이 아니다!!!)
그렇다면 단위벡터를 설정하는 값이 무엇인지 고민할 수 있는데 이러한 질문을 해보겠다. '12'라는 숫자의 가장 작은 단위는? 답은 1이라고 할 수 있다. 우리는 십진법을 기준으로 숫자를 정하므로 가장 작은 단위 1이 12개가 모인 것이 12이기 때문에 1을 단위벡터라고 할 수 있다. 예시로(1,2,3)의 위치에 있는 단위벡터는? 각각의 값을 제곱한 뒤 더하고 루트를 씌워 나온 값을 (1,2,3) 각각에 나눠주면 된다.


왼쪽과 오른쪽의 숨은 그림 찾기? 중간을 기점으로 색이 다르고 디테일한 면에 있어서 조금 다름을 알 수 있다.
위의 사진을 보면 왼쪽의 사진은 빛이 2000W 일 때 오른쪽은 20000W 일 때이다. 우리는 무수한 광선이 이 건물을 비춘다고 상상해 볼 수 있다. 그렇다면 그런 빛을 가지는 벡터의 값은 방향이 있을 것이고 수많은 광선은 방향과 크기를 가지는 벡터 값을 가질 것이다. 이것들을 10배 더 강하게 빛을 비춘다고 할 때 방향은 같지만 단위가 1인 기준이 되는 값을 미리 계산해 놓았다면 10배를 하던 10000배를 하던 단위벡터의 값에 그 값을 곱하면 된다. 위와 같이 단위벡터를 만들어낸 이유는 normal 즉 보통, 기준이 되는 벡터를 구하여 곱셈을 쉽게 하기 위해서라고 생각하면 될 것 같다. 그리고 이제 우리는 벡터를 어떻게 곱하는지 어떻게 나누는지에 대해서 다음에 알아볼 것이다.
벡터를 배우는 이유
1. 우리는 이제 2차원을 넘어서 3차원의 공간에서 생각을 해야 하기 때문에 그 공간에서는 다른 룰 즉 방향성이 있는 벡터를 사용해야 한다. 중요한 것은 3차원이다! 벡터의 곱셈처럼 우리는 3차원에서 뻗어나가는 무언가를 인지하고 계산하기 위해 벡터를 배우는 것이다. 다시 한번 말한다 3차원!
2. 벡터는 어디서 시작했는가가 중요한 것이 아니라 어느 방향으로 얼마큼 움직였는지가 중요하다.