바퀴와 도르래
1) 바퀴
① 1형 바퀴 : 겉 바퀴에 힘이 작용, 힘 이득 예) 자동차 핸들
② 2형 바퀴 : 안바퀴에 힘이 작용, 거리 및 속도 이득 예) 자전거의 뒷바퀴
③ 인체 바퀴 : 거리와 속도를 얻는 2형 바퀴가 대부분 예) 몸통회전
2) 도르래
① 고정도르래 : 방향만 전환
② 이동도르래 : 힘 이득
③ 인체도르래 : 고정도르래만 존재 예) 무릎부위
인체기계의 효율성
1) 지레의 법칙 : F x TFA = R x TRA
2) 인체기계의 역학적 이득과 효율
① 역학적(기계적) 이득(Mechanical Adventage)
MA = 작용된 힘(output force) / 가해진 힘(input force) = R/F
헌데 지레의법칙: F x TFA = R x TRA 이므로 R/F = TFA/TRA
MA = R/F = TFA/TRA
즉, 역학적 이득은 힘과 저항력, 힘팔과 저항팔의 비율로 표시할 수 있다.
② 지레의 역학적 이득
- 1종 지레 : FA < = > RA 이므로 MA < = > 1
- 2종 지레 : FA > RA 이므로 MA > 1
- 3종 지레 : FA < RA 이므로 MA < 1
③ 바퀴의 역학적 이득
- 1종바퀴 : rw(겉바퀴 반경: FA) > Ya(안바퀴의 반경: RA) 이므로 MA > 1
- 2종바퀴 : ra(안바퀴의 반경: FA) < rw(겉바퀴의 반경) 이므로 MA < 1
④ 역학적(기계적) 효율(Mechanical Efficiency)
ME = 실질적 역학적(기계적)이득(AMA) / 이론적 역학적(기계적)이득(TMA)
※ 준비운동을 하는 이유 : 체온을 높임으로써 연골의 활성화, 근섬유 점성도의 활성화 등을 일으켜 결국 인체기계의 역학적(기계적)효율성을 높이기 위해서이다.
- 기계적이익 (MA)
- 1) 이론상의 기계적 이익 (TMA)
- 2) 실제상의 기계적 이익 (AMA)
- 기계적 효율성(ME)
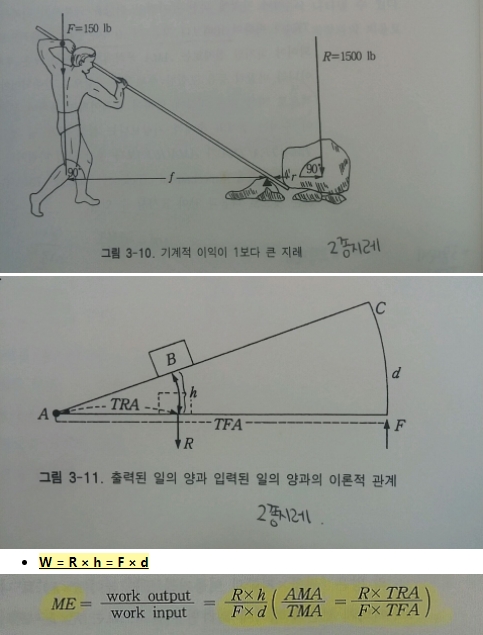
1. 기계적이익
1) 이론상 기계적 이익
- TMA = TFA ÷ TRA
- F x d
- 이론상 기계적 이익 = 힘팔 ÷ 저항팔
2) 실제상 기계적 이익
- AMA = R ÷ F
- R x h
- 실제상 기계적 이익 = 저항 ÷ 힘
2. 기계적 효율성
- ME = AMA ÷ TMA
- 따라서, ( 저항 ÷ 힘 ) ÷ ( 힘팔 ÷ 저항팔 )
- 이걸 치환하면 R × TRA ÷ F × TFA
- 실제상 기계적 이익에서 저항은 부하에 의한 저항뿐만아니라 마찰력 등을 포함한 총체적인 저항으로 간주되어야 한다.
- 따라서 이 수치는 실제의 총체적 저항보다는 항상 작게 될 것이므로 실제적으로는 이론상 기계적 이익이 실제상 기계적 이익보다 항상 크기 마련이다.
- 기계적 일 = 힘 × 작용거리 = 저항 x 실제이동거리