오일러 항등식의 주인공인 오일러는 스위스 출신으로 독실한 종교 집안의 육 남매 중 첫째로 태어났다. 그의 아버지는 사랑하는 아들이 자신의 뒤를 이어 신학을 공부하길 소망했으나, 오일러는 수학을 너무 좋아했고 늘 수학 문제를 해결하는 데 온 힘을 쏟았다.
결국 당대 최고의 수학자 요한 베르누이가 그의 재능을 눈여겨보고 아버지를 설득해 준 덕분에 오일러는 수학 공부를 시작할 수 있었다. 13살의 어린 오일러는 바젤대학교에 입학했고, 석사와 박사학위를 6년 만에 빠르게 마쳤다. 러시아로 온 그는 24살에 물리학과 교수가 되었고, 외국인임에도 러시아에서 수학 교과서를 집필해냈다. 그 외에도 러시아 정부의 요청에 따라 많은 문제를 해결했는데, 그중 하나가 매우 유명한 쾨니히스베르크의 다리 건너기 문제다.
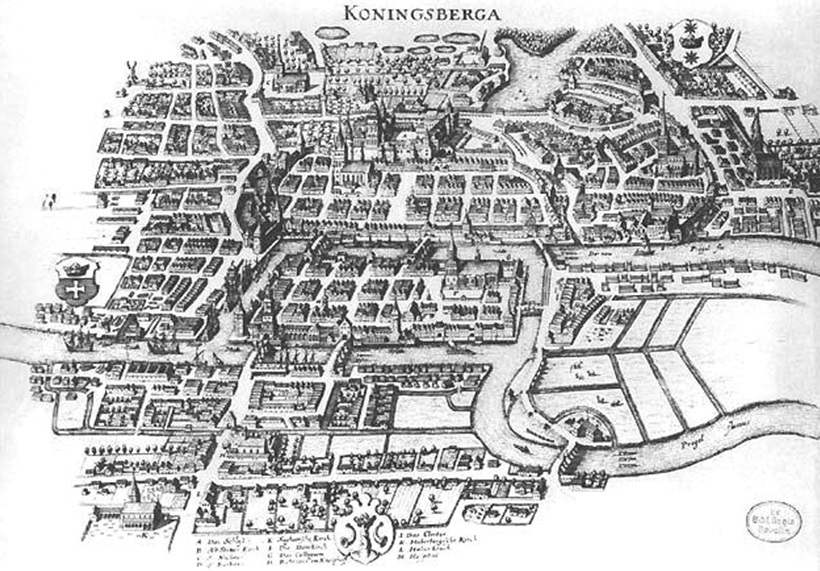
과거 프로이센의 쾨니히스베르크에는 프레겔강이 흐르고 있었다. 강 안에는 섬이 하나 있었고, 섬과 연결된 일곱 개의 다리를 통해 사람들이 섬을 건널 수 있었다. 당시 유명한 도시 전설이 있었는데, 놓여있는 다리를 한 번씩만 건너서 모든 다리를 건널 수 있다는 주장이었다.
성공 여부를 놓고 여러 이야기들이 있었지만, 그 누구도 확실한 수학적 증거나 결론을 제시하지 못했다. 그래서 오일러가 나섰다. 1735년 드디어 오일러가 도시전설 속 이야기를 수학적인 방식을 통해 최초로 증명해냈다. 붓을 종이에서 떼지 않고 한 번에 그려내는 한붓그리기 문제였는데, 쾨니히스베르크의 다리를 모두 거치면서 한 붓으로 그려내는 건 불가능하다는 것을 검증했다.
오일러는 매우 빠른 속도로 논문을 써 내려갔으며, 수학 역사상 가장 많은 글을 남겼다. 수학뿐만 아니라, 물리학, 화학, 생물학, 지구과학, 천문학, 의학, 공학, 식물학, 역사학, 문학 등 다루지 않은 분야가 없었을 정도로 넓은 영역에 거쳐 업적을 남겼다. 나중에는 하루에 4시간씩 자며 남은 시간을 연구에 몰두하다가 두 눈의 시력을 전부 잃었지만, 이후에도 거의 모든 계산을 암산으로 처리하며 훨씬 더 많은 논문을 썼다. 사후 그에게 바치는 추도사에서 한 철학자는 ‘죽음이 드디어 그의 계산을 멈추었다.’라고 애도했을 정도로 오일러에게 계산은 곧 자신의 인생 그 자체였다.
오일러 항등식

우선 오일러 공식이 무엇인지부터 알아보자. 이 공식은 삼각함수와 지수함수의 관계를 매우 간단하게 서술하는 공식으로, 변수의 자리에 π라는 무리수를 넣으면 아주 간단하면서 수학에서 가장 중요한 상수가 모두 등장하는 멋진 식으로 바뀐다. 이걸 오일러 항등식이라고 부른다. 오일러 공식을 이해하기 위해서는 먼저 식에 포함된 상수를 이해해야 한다.
자연상수 'e=2.7183...'

정식 명칭은 아니지만 자연상수라고 많이 부르는 무리수 е는 자연로그의 밑을 뜻한다. 스위스의 수학자 야코프 베르누이는 어느 날 복리 이자를 계산하다가 정해진 기간 내에서 계속 횟수를 올렸더니 값이 특정한 무리수에 수렴한다는 것을 발견했다. 무리수 е의 발견이었다. 이 녀석은 그리 대단한 존재는 아니었는데, 형태를 지수함수로 바꾸었더니 신기하게도 자연현상을 설명할 수 있는 그래프가 그려졌다.
허수 'i, i²=-1'
실수가 아닌 복소수를 뜻하는 허수의 단위는 1572년 이탈리아의 수학자 라파엘 봄벨리가 정의했고, 레온하르트 오일러가 최초로 허수 단위 기호 i를 도입했다. 허수라는 이름은 프랑스의 철학자 르네 데카르트가 실존하지 않는 상상의 수라고 부르며 정착되었는데, 사실 직관적으로 이해하기는 힘들다.

간단히 예를 들어보면, 우리가 거실에 걸린 벽걸이 시계를 보고 있다고 생각해보자. 시곗바늘이 외부로 돌출된 구조로 매우 세련된 디자인이다. 시계의 시침과 분침, 그리고 초침이 가리키는 숫자를 통해 정확한 시간을 알 수 있다. 하지만 아쉽게도 거실 중앙이 아닌 복도나 부엌에 서서 시계를 본다고 가정해보자.
정면에 보이는 시곗바늘을 제대로 보지 못하기 때문에 우리는 그저 옆면이나 아랫면만 보고 현재 시간을 추측할 뿐이다. 돌고 있는 시계 바늘은 매우 제한적인 정보를 제공하며 움직이고, 보이는 시계 바늘의 길이는 시간에 따라 계속 바뀔 것이다. 여기서 쓰이는 것이 바로 허수다. 눈에 직접적으로 보이지 않는 값을 이용해 평면에 정확한 운동 방향이나 위치를 표현할 수 있다.
원주율 'π=3.1415...'

▲
원의 지름에 대한 원 둘레의 비인, 원주율을 나타내는 무리수 π는 영국의 수학자 윌리엄 존스가 처음 사용했고, 오일러로 인해 유명해졌다. π는 원 둘레의 길이로도, 각도로도 표현이 가능한 매우 중요한 수다. π와 i, 그리고 е는 수학에서 가장 중요한 상수들이며, 여기에 0과 1이라는 수학 문제 단골 상수까지 더한 게 바로 오일러 항등식이다. 수학의 중요 상수들이 이렇게 간단해 보이는 수식에 모두 등장해 항등식(항상 참을 만족하는 식)으로 정리된다는 점이 많은 수학자들로부터 놀라운 찬사를 받는 이유다.
궁극의 아름다움을 갖춘 공식의 증명 과정

1748년 출판된 자신의 책 ‘Introductio in analysin infinitorum’에서 오일러는 처음으로 아름다운 공식인 오일러 항등식을 소개했다. 오일러 항등식의 기반이 되는 오일러 공식을 증명하는 방법은 여러가지가 있다. 테일러 전개, 미분, 적분 등 방법은 다양하다.
테일러 전개란, 쉽게 말해 복잡한 여러가지 함수를 다루기 쉬운 다항함수(예 : f(x) = anXn +an-1Xn-1 +…+ a2X2 + a1X + a0)에 가깝게 변형하는 것인데 삼각함수 (cos x, sin x)와 지수함수(ex)로 테일러 전개를 해보면, 비슷한 형태의 식이 나온다. 물론 아무리 닮았다고 해도 이들이 정확하게 어떤 은밀한 관계인지 누구도 의심하지 못했지만, 오일러는 달랐다.
오일러는 과감하게 지수함수의 위치에 복소수를 넣었다. 지수는 실수 범위에서만 정의되기 때문에 당시에는 복소수를 지수로 갖는 함수가 있을 리 없다는 분위기가 만연했는데, 오일러의 용감한 시도로 이제 인류는 방정식으로 대표되는 대수학과 기하학을 통합적으로 이해하는 능력을 갖출 수 있게 되었다.
테일러 전개를 통해 다항함수가 된 지수함수 ex의 지수 부분에 ix를 대입하고, sin x 와 cos x 역시 테일러 전개를 진행하면 놀랍게도 i sin x + cos x =eix 라는 깔끔한 식을 얻을 수 있다. 이게 바로 오일러 공식이다. 엄밀히 말하면 복소수 지수를 정의하는 과정이라고 볼 수도 있겠다. 또한 여기x에 π를 대입하면 미리 밝혔듯이 아름답기 그지없는 오일러 항등식이 나온다. (sin π = 0, cos π = -1 이므로 오일러 항등식 도출)
오일러의 공식은 어디에 쓰일까?

만약 삼각함수와 지수함수의 연결고리를 찾아내지 못했다면, 우리는 오일러 공식을 통해 간단하게 풀 수 있는 문제를 어쩔 수 없이 복잡한 복소수의 계산으로 끙끙거렸을 것이다. 특히 매우 중요하게 사용되는 분야는 양자역학이다. 양자역학에서는 파동성을 갖는 물질을 표현하기 위해 슈뢰딩거의 파동방정식을 사용하는데, 이때 삼각함수가 꼭 필요하다.
또한, 양자역학의 가장 대표적인 특징 중의 하나인 중첩을 수학적으로는 곱하기로 나타내는데, 여기서 파동을 표현한 삼각함수를 곱하기 쉬운 지수함수로 변환하면 계산이 간편해진다. 심지어 미적분도 훨씬 단순해지기 때문에, 파동방정식의 계산 과정에서 거치게 되는 미분과 적분 역시 쉽게 구할 수 있다. 단순히 계산만 간단해진다고 생각하면 오산이다.
이러한 계산은 전부 우리가 실생활에서 양자역학을 활용하기 위해 반드시 필요하며, 만약 양자역학을 제대로 계산해내지 못했다면, 우리는 반도체를 사용할 수 없기 때문에 컴퓨터를 포함해서 대부분의 전자기기는 존재하지 않을 것이다. 마음껏 인터넷을 하거나 웹툰을 보는 것도 불가능했을지도 모른다. 오일러의 공식은 파동의 기술이 매우 중요한 무선통신 분야에서도 없어서는 안 될 소중한 공식이기 때문이다.

오일러 공식을 다른 관점에서 바라보면, 복소평면에서 일정한 속도로 원운동을 하는 물체의 위치 방정식이라고도 볼 수 있다. 이를 전자공학적인 측면에서 보면, 전기를 만들어내는 과정에서 회전하는 코일에 의해 순간적으로 유도되는 전류가 어떻게 바뀌어 나가는지를 나타낸다. 이처럼 아주 기본적인 전기의 흐름에서조차 오일러의 공식은 꽤 훌륭한 역할을 맡고 있다.
세상에서 가장 아름답고 우아했던 장면 가운데 하나를 떠올린다면 2010년 밴쿠버 동계올림픽에서 보여준 김연아 선수의 무결점 연기다. 피겨스케이팅 역사상 가장 위대한 미의 결정체였으며, 그녀는 피겨 여자 싱글 사상 최고점으로 금메달을 따냈다. 그녀의 완벽한 몸짓은 피겨스케이팅을 전혀 모르는 문외한이라도 감동이 차오를 수밖에 없었고, 투명한 빙판 위에서 보여준 그녀의 환상적인 움직임은 채점 방식에 대한 이해도와 무관하게 박수가 절로 나왔다. 그저 무한히 아름다웠기 때문이다. 수식과 비교할 수 없는 건 당연하지만, 오일러 공식 역시 그러하다. 공식에 대한 수학적 이해가 뒷받침되지 않더라도 이미 충분히 아름답다. 물론 그 세밀한 상수 조각의 품격을 느끼기 위해서는 더 많이 알면 알수록 이득이겠지만, 아마도 오일러 공식의 아름다움을 느끼기에는 충분할 것이다.